An aircraft executes a horizontal loop with a speed of 150 m/s with its, wings banked at an angle of 12∘. The radius of the loop is (g=10m/s2)
10.6km
9.6 km
7.4 km
5.8 km
The correct Answer is:A
To find the radius of the loop executed by the aircraft, we can use the formula for the banking angle in circular motion. The formula is given by:
tan(θ)=V2Rg
Where:
- θ is the banking angle,
- V is the speed of the aircraft,
- R is the radius of the loop,
- g is the acceleration due to gravity.
Given:
- V=150m/s
- θ=12∘
- g=10m/s2
We need to find the radius R.
Step 1: Convert the angle to radians (if necessary)
In this case, we can directly use the angle in degrees since we will be using the tangent function.
Step 2: Calculate tan(12∘)
Using a calculator or trigonometric tables, we find:
tan(12∘)≈0.2126
Step 3: Substitute the values into the formula
We can rearrange the formula to solve for R:
R=V2g⋅tan(θ)
Substituting the known values:
R=(150)210⋅0.2126
Step 4: Calculate R
Calculating the numerator:
(150)2=22500
Calculating the denominator:
10⋅0.2126=2.126
Now substituting these values back into the equation for R:
R=225002.126≈10563.5m
Final Answer
The radius of the loop is approximately 10563.5m.
---
- θ is the banking angle,
- V is the speed of the aircraft,
- R is the radius of the loop,
- g is the acceleration due to gravity.
- V=150m/s
- θ=12∘
- g=10m/s2
In this case, we can directly use the angle in degrees since we will be using the tangent function.
Using a calculator or trigonometric tables, we find:
We can rearrange the formula to solve for R:
Calculating the numerator:
The radius of the loop is approximately 10563.5m.
Topper's Solved these Questions
Similar Questions
Knowledge Check
An aeroplane executes a horizontal loop at a speed of 720 kmph with its wings banked at 45°. What is the radius of the loop? (Take g = 10 ms−2 )
A7.2 kmB4 kmC2 kmD4.5 kmA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
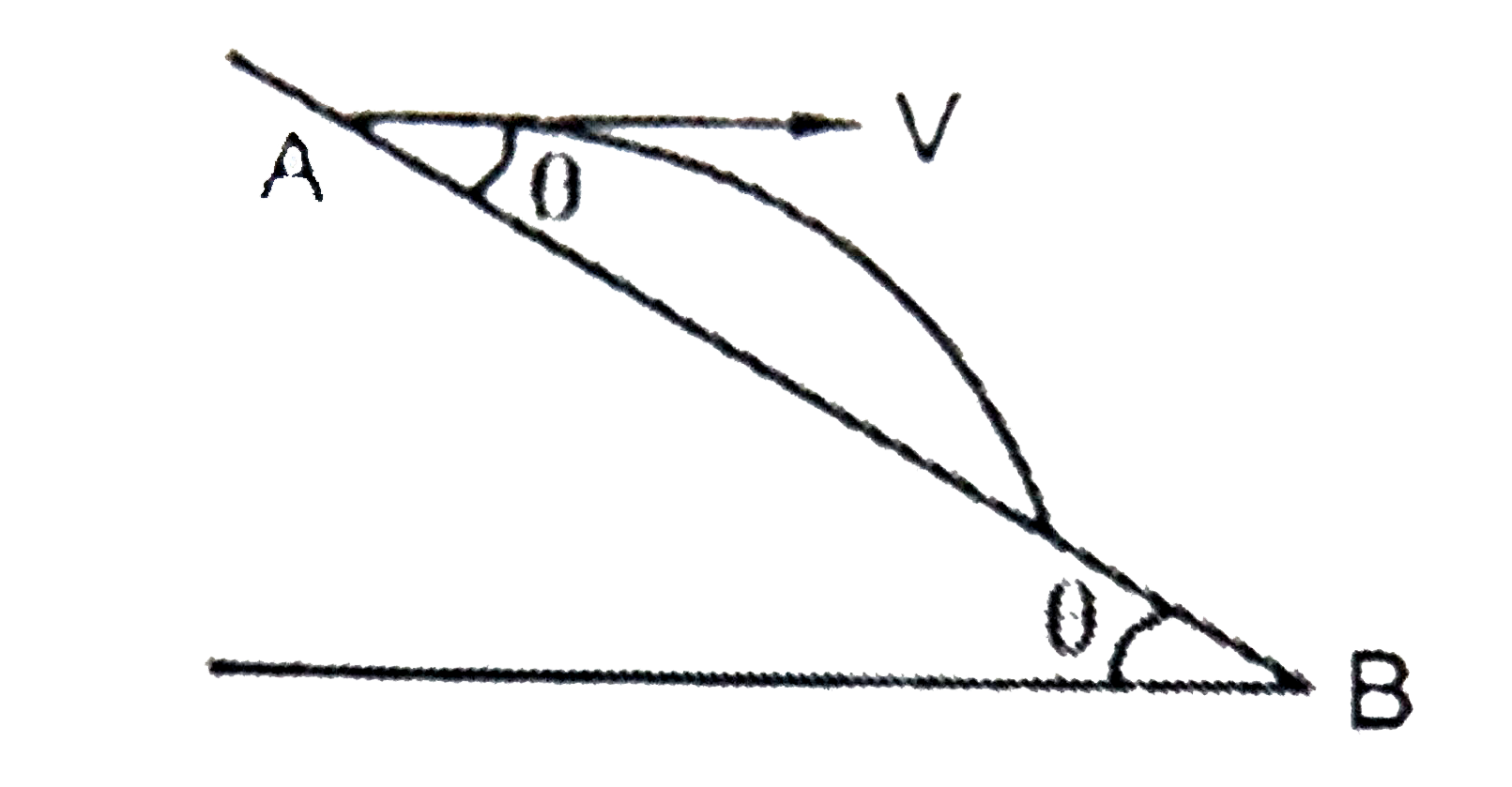
Find the time taken by the particle to hit the plane.A34sB3sC4sD43sA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

What is the velocity of the particle just before it hits the plane?A5√3m/sB52√13m/sC10√13m/sD5√26m/s
An aircraft executes a horizontal loop at a speed of 540 km/h with its wings banked at 45∘. What is the radius of the loop?
View SolutionAn aircraft executes a horizontal loop at a speed of 720kmh−1 , with its wings banked at 15∘ What is the radiue of the loop ?
View SolutionAn aircraft executes a horizontal loop of radius 1 km with a steady speed of 900kmh−1. Compare its centripetal acceleration with the acceleration due to gravity.
View SolutionAn air craft executes a horizontal loop of radius 1km with s steady speed of 900kmh−1. Compare its centripetal acceleration with the acceleration due to gravity.
View SolutionA jet aircraft flies at a speed of 410m/s. What is this speed known as?
View Solution