Hydrogen atom in its ground state, is excited by means of monochromatic radiation of wavelength 975 Å . How many different lines are possible in the resulting spectrum ? Calculate the longest wavelength amongst them. Given, ionisation energy of hydrogen atom is 13.6 eV. Solution in Bengali
Wavelength of incident radiation,
λ=975Å=975×10−8 cm
∴ Energy of this photon,
hf=hcλ
=6.625×10−27×3×1010975×10−8erg
=6.625×10−27×3×1010975×10−8×1.6×10−12eV=12.74eV
Ionisation energy of hydrogen atom =13.6 ev., the ground state energy of this atom =-13.6 eV . so, the energy of the excited state in which the atom is raised under the influence of incident radiation =-13.6+12.74=-0.86 eV.
The quantum number in the ground state = 1. so, if the quantum number in the excited state be n then
−0.86=−13.6n2or,n2=13.60.86=16(approx.)
so, n =4, i.e the excited state is the fourth Bohr orbit.
During transition from the fourth Bohr orbit to the ground state , the decrease in energy of the atom may occur in 6 different ways
[Fig.1.11] . As a result ,6 lines will be obtained in the spectrum.
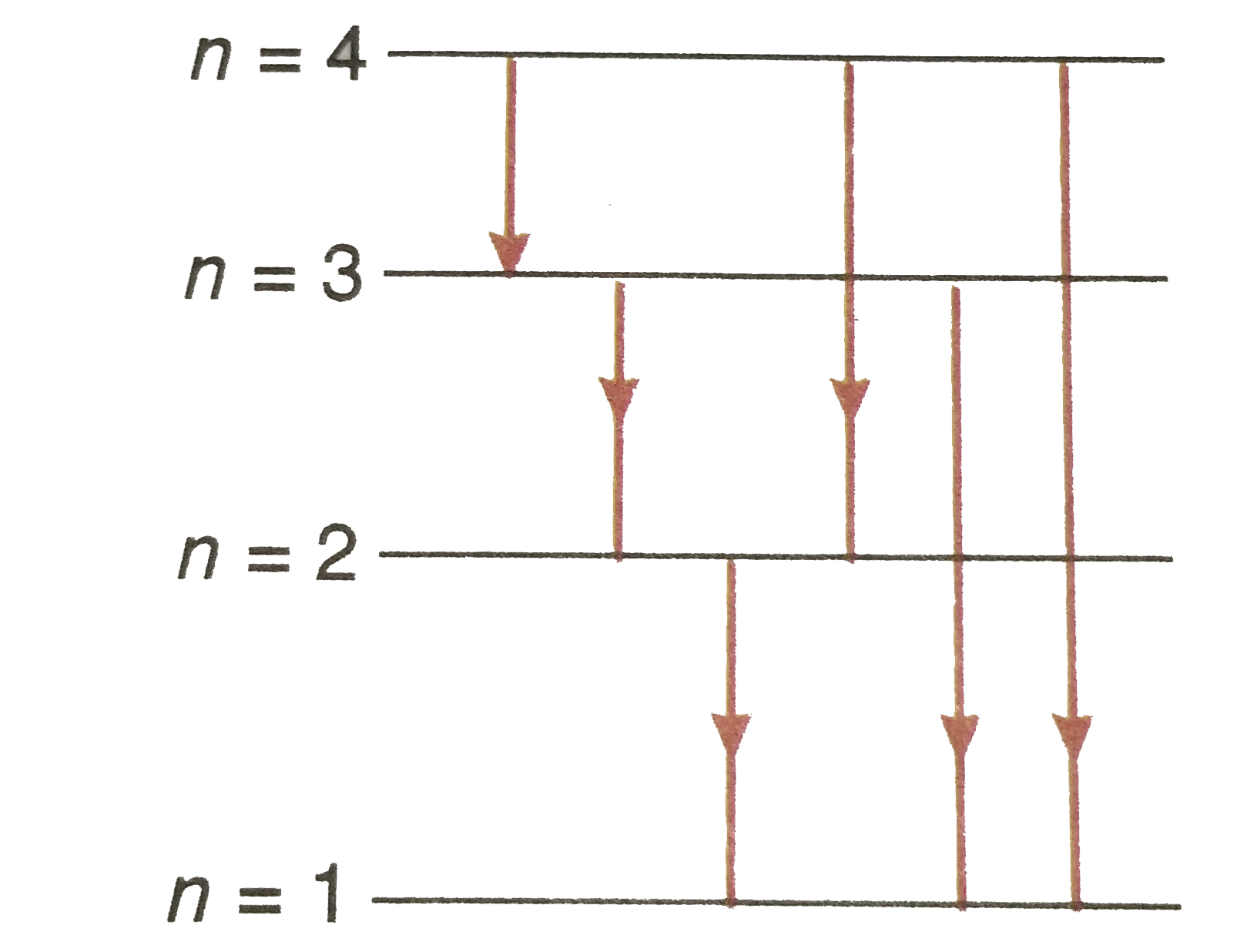
Of them, during transition from n=4 to n=3 , the energy difference is the least and hence in this case, the wavelength of the emitted spectral line will be maximum.
Energy of the third Bohr orbit =-13.632=−1.51eV
∴ Decrease in energy due to transition form n =4 to n=3 =-0.86 -(-1.51)=0.65 eV.
Hence, the relation hf =hcλ=E4−E3 gives,
λ=hcE4−E3=6.625×10−27×3×10100.65×1.6×10−12=19110×10−8cm=19110Å
Topper's Solved these Questions
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - Section Related Questions
18 Videos
- ATOMBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMEXERCISE - Higher Order Thinking Skill (Hots ) Questions
22 Videos
- ALTERNATING CURRENT BOOK - CHHAYA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CBSE SCANNER
33 Videos
- ATOMIC NUCLEUSBOOK - CHHAYA PUBLICATIONCHAPTER - ATOMIC NUCLEUSEXERCISE - CBSE SCANNER
14 Videos
Similar Questions
Discuss briefly the main inferences made by Rutheford from his α -particle scattering experiment.
View SolutionElectron of a hydrogen atom revolves in 3rd orbit.
Find the angular momentum of the electron.
(h=6.6×10−27erg⋅s)
View SolutionMention the two characteristic properties of the material suditable for making core of a transformer.
View SolutionDraw a plot of potential energy of a pair of nucleons as a function of their separations. Mark the regions where the nuclear force is (i)attactive and (ii)repulsive . Write any two characteristic features of nuclear forces.
View SolutionHydrogen atom is ground state is excied by mean of monochromatic radiation of wavelength 975Å How many asume different lines are possible is the resulting spactrum ? Calculate the lorgest energy for hydrogen atom as 13.6 eV
View SolutionHydrogen atom is its ground state is excited by means of monochromatic radiation of wavelength 1023 Å . How many different lines are possible in the resulting spectrum? Calculate the longes wavelength among them. You may assume the ionization energy of hydrogen atom as 13.6 eV.
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of λ=975Å. Number of spectral lines in the resulting spectrum emitted will be
View SolutionHydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength 970.6Å. How many lines are possible in the resulting emission spectrum ? Calculate the longest wavelength amongst them. You may assume that the ionisation energy for hydrogen atom is 13.6 eV. Given Planck's constant =6.6×10−34Js, c=3×10(8)ms−1
View SolutionHow many hydrogen atoms in the ground state are exited by means of monochromatic radiation of wavelength 970.6 Ã…. How many different lines are possible in the resulting emission spectrum? Find the longest wavelength among these .
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of lambda=975"Å" . Number of spectral lines in the resulting spectrum emitted will be
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of λ=975Å. Number of spectral lines in the resulting spectrum emitted will be
View SolutionA hydrogen atom in the ground state is excited by radiations of wavelength 975 Å.
Find : (a) the energy state to which the atom is excited
(b) how many lines will be possible in emission spectrum
View SolutionThe hydrogen atom in the ground state excited by means of light of lambda=975 Å. How many different lines are possible in resultant spectrum ?
View SolutionHydrogen atom in its ground state is excited by means of a monochromatic radiation of wavelength 970.6 Å. How many different transitions are possible in the resulting emission spectrum? Find the longest wavelength amongst these. (lonisation energy of hydrogen atom in its ground state is 13.6 eV and take h=6.6xx10^(-34)Js) Data : Wavelength of incident radiation = 970.6 Å = 970.6 X 10^(-10)m Ionisation energy of hydrogen atom in its ground state = 13.6 eV (i) Number of possible transitions = ? (ii) Longest wavelength emitted = ?
View SolutionA monochromatic radiation of wavelength 975Å excites the hydrogen atom from its ground state to a higher state . How many different spectral lines are possivle in the resulting spectrum ? Which transition corresponds to the longest wavelenght amongst them ?
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of lambda = 975 Å. Number of spectral lines in the resulting spectrum emitted will be
View Solution
