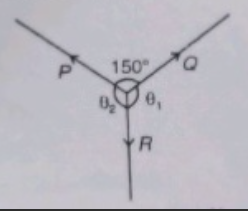
P, Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1.9318kg−wt,sinθ1=0.9659, the value of R is (∈kg−wt)
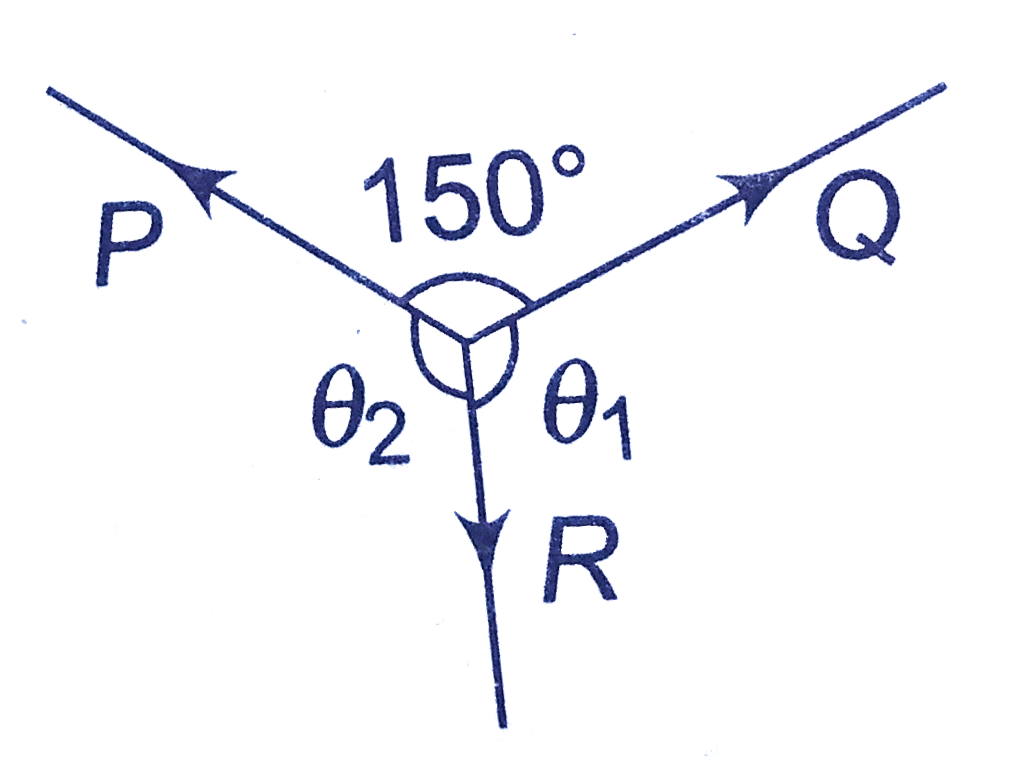
Psinα=Qsinβ=Rsinγ
Pcosα=Qcosβ=Rcosγ
Ptanα=Qtanβ=Rtanγ
Psinβ=Qsinγ=Rsinα
The correct Answer is:A
Step by step video, text & image solution for P, Q and R are three coplanar forces acting at a point and are in equilibrium. Given P= 1.9318 kg-wt, sin theta_(1)= 0.9659, the value of R is (in kg-wt) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Three forces of magnitude 30, 60 and P acting at a point are in equilibrium. If the angle between the first two is 60∘, the value of P is
A30√7B30√3C20√6D25√2Three forces of magnitude 30, 60 and P acting at a point are in equilibrium. If the angle between the first two is 60∘, the value of P is
A30√7B30√3C20√6D25√2The greatest and least resultant of two forces acting at a point are 29kgwt. and 5kgwt. respectively . If each force is increased by 3kgwt. the magnitude of the resultant of new forces acting at right angles to each other is
A45kgwt.B35kgwt.C25kgwt.D15kgwt.
ABC is a triangle. Forces P, Q, R acting along the lines OA, OB and OC are in equilibrium. Then P:Q:R= …..
If O is the incentre of ΔABC
View SolutionABC is a triangle. Forces P, Q, R acting along the lines OA, OB and OC are in equilibrium. Then P:Q:R= …..
If O is the centroid of the triangle ABC
View SolutionABC is a triangle. Forces P, Q, R acting along the lines OA, OB and OC are in equilibrium. Then P:Q:R= …..
If O is the circumcentre of the triangle ABC.
View SolutionTwo forces P and Q act at an angle of 120∘ with each other. If the resultant is at right angles to P and P is equal to 4kg−wt, then the value of Q is
View SolutionLet a, b and c be three non-zero and non-coplanar vectors and p, q and r be three given by →p=→a+→b−2→c,→q=3→a−2→b+→c and r=→a−4→b+2→c. If the volume of the parallelopiped determined by→a,→band→c is V1 and that of the parallelopiped determined by →p,→qand→r is V2, then V2:V1=
View Solution