If ∣∣→V1+→V2∣∣=∣∣→V1−→V2∣∣ and V2 is finite, then
V1 is parallel to V2
→V1=→V2
V1 and V2 are mutually perpendicular
∣∣→V1∣∣=∣∣→V2∣∣
The correct Answer is:C
To solve the problem, we need to analyze the condition given:
|→V1+→V2|=|→V1−→V2|
Step 1: Square both sides
To eliminate the absolute values, we square both sides of the equation:
|→V1+→V2|2=|→V1−→V2|2
Step 2: Expand both sides
Using the property of magnitudes, we can expand both sides:
(→V1+→V2)⋅(→V1+→V2)=(→V1−→V2)⋅(→V1−→V2)
This leads to:
→V1⋅→V1+2→V1⋅→V2+→V2⋅→V2=→V1⋅→V1−2→V1⋅→V2+→V2⋅→V2
Step 3: Simplify the equation
Now, we can simplify the equation:
|→V1|2+2→V1⋅→V2+|→V2|2=|→V1|2−2→V1⋅→V2+|→V2|2
Step 4: Cancel common terms
We can cancel |→V1|2 and |→V2|2 from both sides:
2→V1⋅→V2=−2→V1⋅→V2
Step 5: Combine like terms
This simplifies to:
4→V1⋅→V2=0
Step 6: Conclusion
From this equation, we conclude:
→V1⋅→V2=0
This implies that the vectors →V1 and →V2 are perpendicular to each other.
Thus, the final answer is that →V1 and →V2 are mutually perpendicular.
To eliminate the absolute values, we square both sides of the equation:
Using the property of magnitudes, we can expand both sides:
Now, we can simplify the equation:
We can cancel |→V1|2 and |→V2|2 from both sides:
This simplifies to:
From this equation, we conclude:
Topper's Solved these Questions
Similar Questions
Find 3-dimensional vectors →v1,→v2,→c3 satisfying →v1.→v2=4,→v1.→v2=−2,→v1.→v3=6
→v2.→v2=2,→v2.→v3=−5,→v3.→v3=29
View SolutionAssertion : An object has given two velocities →v1 and →v2 has a resultant velocity →v=→v1+→v2.
Reason : →v1and→v2 should be velocities with reference to some common reference frame.
View Solution
Knowledge Check
If |vecV_1+vecV_2|=|vecV_1+vecV_2|andV_2 is finite, then
AV1 is parallel to V2B→V1=→V2CV1 and V2 are mutually perpendicularD∣∣→V1∣∣=∣∣→V2∣∣Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
A1B4C0DNone of theseAssertion: An observer is moving due east and wind appears him to blow from north. Then the actual direction of air blow must be towards south-east
Reason: →VR=→VA−→VM where →VR is the relative velocity of wind w.r.t. man. →VA= actual velocity of wind (w.r.t. ground) and →VM= velocity of man w.r.t. ground.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are false
Let →a→band→c be non- zero vectors aned →V1=→a×(→b×→c)and→V2=(→a×→b)×→c.vectors →V1and→V2 are equal . Then
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is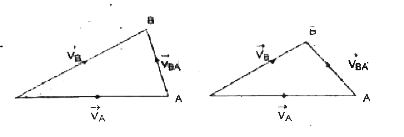
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A river is flowing from west to east at a speed of 5 m/s. A man on the south bank of the river, capable of swimming at 10 m/s in still water, wants to cross the river without drifting, he. should swim
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 respectively at time t= 0. They collide at time t0. Their velocities become →v1 and →v1 at time 2t0 while still moving in air. The value of ∣∣(m1→v11+m2→v12)−(m1→v1+m2→v2)∣∣ is
View SolutionConsider three vectors →v1=→v2−→v3,→v1,→v2and→v3 such that If →v1=(→a׈i)׈i,→v2=(→a׈j)׈jand→v3=(→a׈k)׈k, where →a is non -zero vector then :-
View Solution
