If vectors →P,→Q and →R have magnitude 5,12 and 13 units and →P+→Q=→R, the angle between →Q and →R is :
A
cos−1(5/12)
B
cos−1(5/13)
C
cos−1(12/13)
D
cos−1(2/13)
Video Solution
Text Solution
The correct Answer is:C
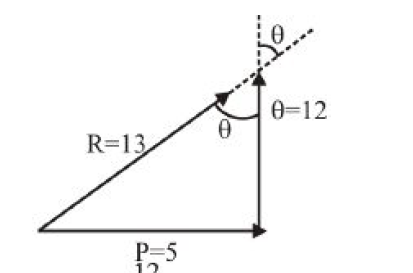
cosθ=1213
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
Acos−1(512)Bcos−1(513)Ccos−1(1213)Dcos−1(213)If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
Acos−1(512)Bcos−1(513)Ccos−1(1213)Dcos−1(213)If →P.→Q=PQ then angle between →P and →Q is
A0∘B30∘C45∘D60∘
If ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
View SolutionIf →P−→Q−→R=0 and the magnitudes of →P,→Qand→R are 5 , 4 and 3 units respectively, the angle between →Pand→R is
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
View Solutionif →P+→Q=→P−→Q, then
View SolutionThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View Solution
