Tangents PA and PB are drawn to $x^{2} + y^{2} = 4$ from the point $P (3, 0)$ . Area of triangle PAB is equal to:-

A

$\frac{10}{9} \sqrt{5}$ sq. units

B

$\frac{20}{3} \sqrt{5}$ sq. units

C

$\frac{5}{9} \sqrt{5}$ sq. units

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation circle : $x^{2} + y^{2} = 4$

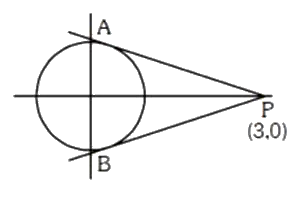
Equation of AP : $y = m (x - 3)$
$y - m x + 3 m = 0$
circel of circle: (0,0)
radius : 2
length of perpendicular distance = radius
$\frac{3 m}{\sqrt{1 + m^{2}}} = 2$
$\Rightarrow 9 m^{2} = 4 + 4 m^{2}$
$\Rightarrow m = \pm \frac{2}{\sqrt{5}}$
BP: $y = \frac{2}{\sqrt{5}} (x - 3) & A P : y = - \frac{2}{\sqrt{5}} (x - 3)$
Now, $x^{2} + \frac{4}{5} {(x - 3)}^{2} = 4$
$\Rightarrow 5 x^{2} + 4 x^{2} + 36 - 24 x = 20$
$\Rightarrow 9 x^{2} - 24 x + 16 = 0$
$∴ {(3 x - 4)}^{2} = 0$
$\Rightarrow x = \frac{4}{3}, y = - \frac{2 \sqrt{5}}{3}$
$\Rightarrow B (\frac{4}{3}, - \frac{2 \sqrt{5}}{3}) & A (\frac{4}{3}, \frac{2 \sqrt{5}}{3})$
Area of $Δ P A B = \frac{1}{2} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} 3 & 0 & 1 \frac{4}{3} & \frac{2 \sqrt{5}}{3} & 1 \frac{4}{3} & - \frac{2 \sqrt{5}}{3} & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣$
$= \frac{1}{2} ∣ ∣ ∣ ∣ 3 (\frac{4 \sqrt{5}}{3}) + 1 (- \frac{8 \sqrt{5}}{9} - \frac{8 \sqrt{5}}{9}) ∣ ∣ ∣ ∣$
$= \frac{1}{2} ∣ ∣ ∣ 4 \sqrt{5} - \frac{16 \sqrt{5}}{9} ∣ ∣ ∣ = \frac{10 \sqrt{5}}{9}$ .

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One or More
If tangents PA and PB are drawn from $P (- 1, 2)$ to $y^{2} = 4 x$ then
AEquation of AB is $y = x - 1$
BLength of AB is 8
CLength of AB is 4
DEquation of AB is $y = x + 1$
Question 2 - Select One
From a point P perpendicular tangents PQ and PR are drawn to ellipse $x^{2} + 4 y^{2} = 4$ , then locus of circumcentre of triangle PQR is
A $x^{2} + y^{2} = \frac{16}{5} {(x^{2} + 4 y^{2})}^{2}$
B $x^{2} + y^{2} = \frac{5}{16} {(x^{2} + 4 y^{2})}^{2}$
C $x^{2} + 4 y^{2} = \frac{16}{5} {(x^{2} + y^{2})}^{2}$
D $x^{2} + 4 y^{2} = \frac{16}{5} {(x^{2} + y^{2})}^{2}$
Question 3 - Select One
Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?
A $f (x) = 4$ has real roots.
B $f (x) = 1$ has real roots.
CThe range of $y = f^{- 1}$ is $[- \frac{π}{4} + 2, \frac{π}{4} + 2]$
DNone of these

Recommended Questions

Home
Ask Doubt
Profile