The statement:
~((~p∧q)∨(p∧~q)∨(p∨q)) is equivalent to
A
p∨q
B
~p∧~q
C
~p∨~q
D
p∧q
Video Solution
Text Solution
The correct Answer is:B
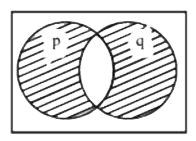
(~p∧q)∨(p∧~q)≡(p∨q)∧~(p∧q)
⇒(~p∧q)∨(p∧~q)∨(p∨q)≡(p∧q)
⇒((~p∧q)∨(p∧~q)∨(p∨q))≡p∧~q
|
Similar Questions
Knowledge Check
p∧~q is equivalent to
A~(p→q)B~(q→p)C(q→p)D(p→q)The statement ~(p∧q)∨q) :
Ais a tautologyBis equivalent to (p∧q)∨~qCis equivalent to p∨qDis a contradictionThe statement pattern (p∧q)∧[(p∧q)]∨(−p∧q) is equivalent to . .......
Ap∨qBqCp∧qDp
The logical statement
[~(~p∨q)∨(p∧r)∧(~q∧r)]
is equivalent to
View Solution(p∧q)→((r∧q)∧p) is a
View SolutionThe statement p→(~q) is equivalent to
View SolutionLet P and q be two statements,
then ~(~p∧q)∧(p∨q) is
logically equivalent to
View SolutionFor any two statements p and q, the statement
~(p∧q)∨(~p∧q)
is equivalent to
View Solution

