The area bounded by the curve y=x2+4x+5, the axes of co-ordinates & the minimum ordinate is:
A
323 sq. unit
B
423 sq. unit
C
523 sq. unit
D
83 sq. unit
Video Solution
Text Solution
The correct Answer is:B
y=x2+4x+5=(x+2)2+1
A=∫0−2(x2+4x+5)dx=x33+2x2+5]02
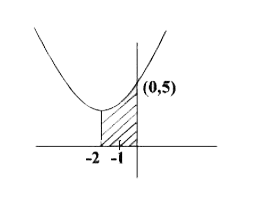
−[−83+8−10]=2+83=143=423.
|
Similar Questions
Knowledge Check
The area bounded by the curve y=x2+4x+5, the axes of co ordinates and the minimum ordinate is
A323 sq.unitsB423 sq.unitsC523 sq.unitsD83 sq.unitsThe area bounded by the curve y = log x, X- axis and the ordinates x = 1, x = 2 is
Alog 4 sq. unitsBlog 2 sq. unitsC(log 4 - 1) sq. unitsD(log 4 + 1 ) sq. unitsArea bounded by the curve y=x3, the x-axis and the ordinates x=−2andx=1 is
A-9B−154C154D174
Find the area bounded by the curve y=logx, x-axis and the ordinates x=1&x=e.
View SolutionFind the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionFind the area bounded by the curve y=x|x|, x-axis and ordinates x=−1 and x=1.
View SolutionArea bounded by the curve y=x2, the x-axis and the ordinates x=−2andx=1 is :
View SolutionThe area bounded by the curve y=x|x|, x-axis and the ordinates x=1,x=-1 is given by
View Solution

