Three particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
√3GMa,2π√a23GM
√GMa,12π√3GMa3
√GMa,2π√a33GM
√GM3a,2π√a33GM
The correct Answer is:C
The resultant force on each particle due to other two particles is,
FR=√F21+F22+2F1F2cosθ=√3F1
=√3GM2a2 …(i)
If each particle is given a tangential velocity v, so that F acts as the centripetal force, they will move in a circle of radius,
r=(23)asin60∘=a√3

Now, FR=Mv2r=√3Mv2a ...(ii)
From eqn. (i) and (ii),
√3Mv2a=GM2√3a2 or v=√GMa
Time period,
T=2πrv=2πa√3√aGM=2π√a33GM
Topper's Solved these Questions
Similar Questions
Three parties, each of mass m, are situated at the vertices of an equilateral triangle of side length a . The only forces acting on the pariclaes are th eir mutual gravitational forces. It is desired that each particles moves ina a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of teh circular motion.
View SolutionThree particles, each of mass m, are situated at the situated at the vertices of an equilateral triangle of side 'a'. The only forces acting on the particles are their mutual gravitational forces. It is intended that each particle moves along a circle while maintaining their original separation 'a'. Determine the initial velocity that should be given to each particle and the time period of the circular motion. The resultant force on particle at A due to other two particles is
View Solution
Knowledge Check
Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
AzeroB3GML2C9GML2D12GM√3L2Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
AzeroB3GML2C9GML2D2GML2Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
A2G2m2LBGm22LC3Gm22LD3Gm2L
Three particles, each of mass m, are situated at the vertices of equilateral triangle of side length a. The only forces. It is desired that each particle moves in a circle while maintaining the original mutual speration a. Find the intial velocity that should be given to each particle and also the time period of the circular motion.
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
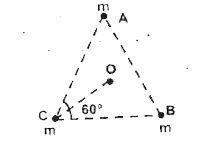
The gravitational potential at O is
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
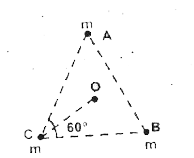
Force acting on particle C, due to particle A and B
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution

