Question

एक समतल उत्तल लेंस के समतल पृष्ठ पर चांदी की कलई करने पर लेंस फोकस दूरी 20 सेमी वाले अवतल दर्पण की भांति व्यवहार करता है तथा उत्तल पृष्ठ पर चांदी की कलई करने पर वह फोकस दूरी 7 सेमी वाले अवतल दर्पण की भांति व्यवहार करता है | लेंस के पदार्थ का अपवर्तनांक ज्ञात कीजिए |

Explanation

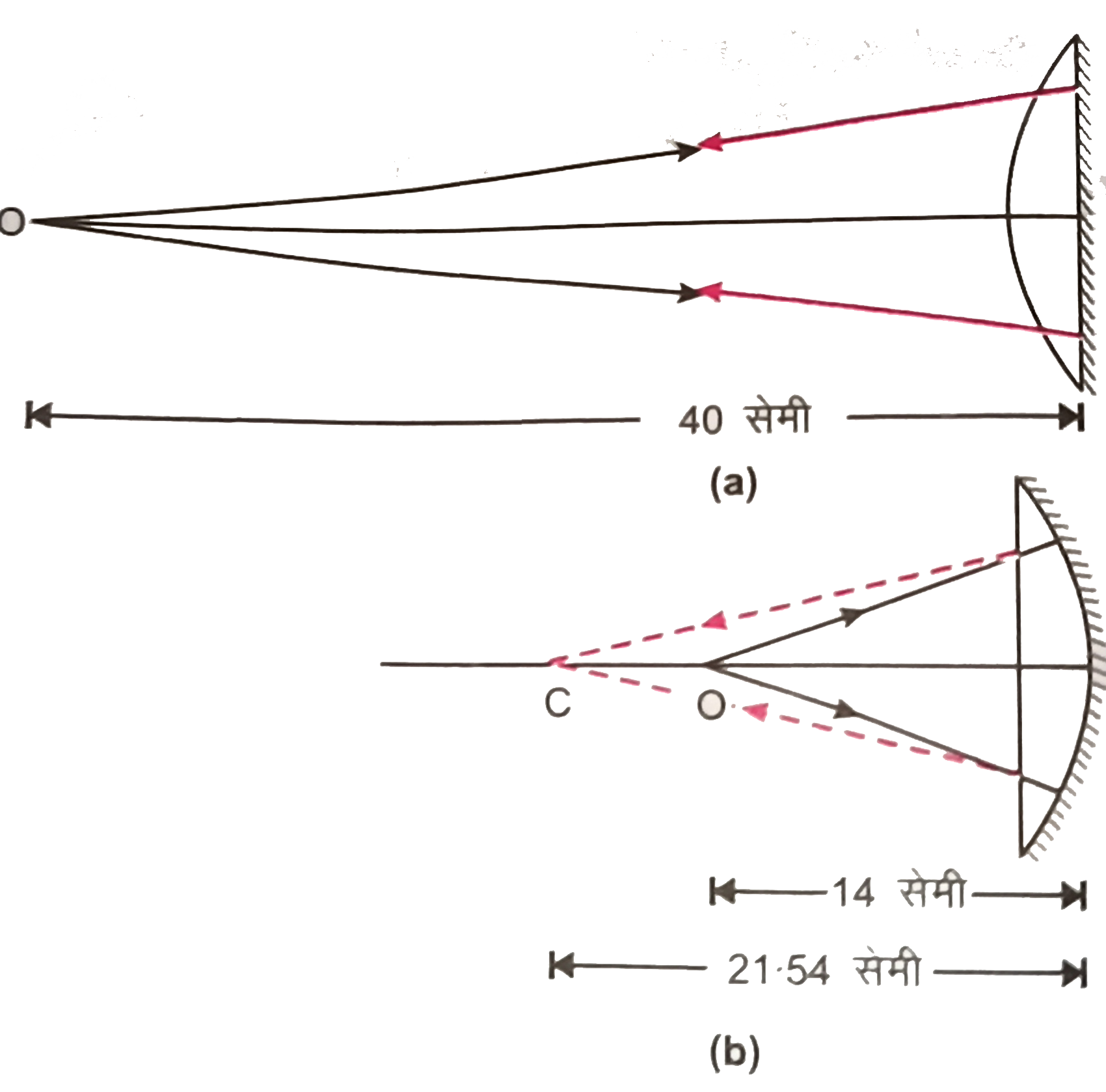
प्रश्नानुसार, समतल-उत्तल लेंस के समतल पृष्ठ पर चांदी की कलई करने पर लेंस अवतल दर्पण की भांति व्यवहार करता है जिसकी वक्रता त्रिज्या `=2xx` फोकस दूरी `=2xx20 =40` सेमी है अर्थात इससे दूरी 40 सेमी पर रखी वस्तु O का प्रतिबिंब उसी स्थान पर बनता है | ऐसा तभी संभव है जबकी वस्तु से अब आपतीत किरणे लेंस के वक्र पृष्ठ से अपवर्तित होकर समतल पृष्ठ पर लंबवत पड़े [चित्र 9.76 (a)] अर्थात बिंदु O लेंस का फोकस बिंदु हो | अतः इस स्थिति में लेंस की फोकस दूरी =40 सेमी |
अब लेंस के उत्तर पृष्ठ पर चांदी की कलई करने पर लेंस अवतल दर्पण की भांति व्यवहार करता है जिसकी वक्रता त्रिज्या `=2xx` फोकस दूरी `=2xx7=14` सेमी है अर्थात अब इससे दुरी 14 सेमी पर स्थित वस्तु O का प्रतिबिंब उसी स्थान पर बनता है | ऐसा तभी संभव है जबकी वस्तु से आपतित किरणें लेंस के वक्र पृष्ठ से अपवर्तित होकर उत्तल पृष्ठ पर लंबवत पड़े | उत्तल पृष्ठ पर आपतित ये लंबवत किरणे पीछे बढ़ाने पर वक्रता केंद्र C(दूरी R) से आती प्रतीत होगी [चित्र 9.76 (b)], अर्थात O पर स्थित वस्तु का प्रतिबिंब, लेंस से अपवर्तन द्वारा C पर बनता है |
तब u=14 सेमी (ऋणात्मक), v=R (ऋणात्मक), f=40 सेमी |
सूत्र `(1)/(v) -(1)/(u) =(1)/(f)" से, "(1)/((-R)) -(1)/((-14))=(1)/(40)" या "(1)/(R) =(13)/(280)`
अब लेंस के सूत्र `(1)/(f) =(mu -1) ((1)/(R_(1))-(1)/(R_(2)))" में "R_(1) =R" तथा "R_(2)=oo` रखने पर,
`therefore " "(1)/(40) =(mu -1) ((13)/(280)-(1)/(oo))`
या `" "(mu-1)=(1)/(40) xx(280)/(13) =(7)/(13)`
या `" "mu =1+(7)/(13)=(20)/(13) =1 cdot 54`