आवेश q से आवेशित एक कण परस्पर लम्बवत् एकसमान क्षेत्रों में इन दोनों क्षेत्रों के लम्बवत् वेग से प्रवेश करता हैं तथा के परिमाण या दिशा में बिना किसी परिवर्तन के बाहर निकलता है , तो :
.
आवेशित कण पर कुल बल
अब
= - क्योंकि (
चूँकि तथा परस्पर लम्बवत् हैं , अत: तथा
Topper's Solved these Questions
- गतिमान आवेश एवं चुम्बकत्वBook:SHIVLAAL PUBLICATIONChapter:गतिमान आवेश एवं चुम्बकत्वExercise:आंकिक प्रश्न
Explore 8 Videos
- किरण प्रकाशिकी एवं प्रकाशिक यन्त्र Book:SHIVLAAL PUBLICATIONChapter:किरण प्रकाशिकी एवं प्रकाशिक यन्त्र Exercise:वस्तुनिष्ठ प्रश्न
Explore 105 Videos
- चुम्बकत्व एवं द्रव्य Book:SHIVLAAL PUBLICATIONChapter:चुम्बकत्व एवं द्रव्य Exercise:इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओ के लिए ( वस्तुनिष्ट प्रश्न )
Explore 72 Videos
Similar Questions
त्रिज्या 10 सेमी के वृत्तीय धारावाही लूप के केंद्र पर उत्पन्न चुम्बकीय क्षेत्र , उस स्थान पर पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक से संतुलित हो जाता है । यदि H=4⋅0×10−5 टेसला हो , तो लूप में धारा का मान ज्ञात कीजिए ।
View Solutionदो समतल दर्पण एक-दूसरे से कोण θ पर झुके है | प्रथम दर्पण पर आपतन कोण 50∘ बनाती किरण, परावर्तन के बाद दूसरे दर्पण पर पड़ती है, जहाँ से यह प्रथम दर्पण पर आपतित किरण के समान्तर परावर्तित होती है | दोनों दर्पणों के बीच कोण θ है :
View Solutionचुम्बकीय क्षेत्र B की क्षेत्र रेखाओ से संबंधित कथन नहीं है
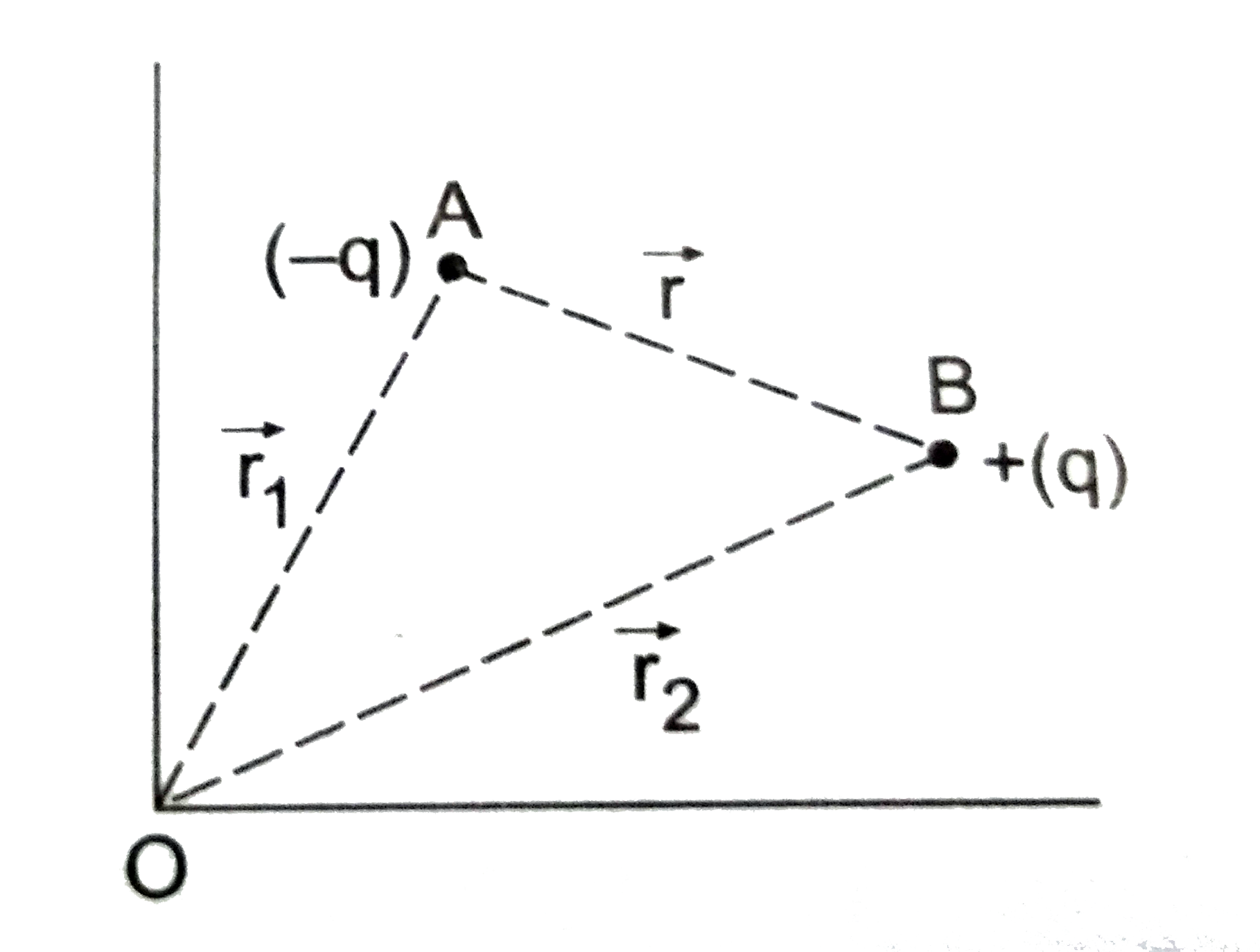
View Solutionकिसी विद्युत व्दिध्रुव का नेट आवेश शून्य होता हैं , लेकिन इसका व्दिध्रुव - आपूर्ण अशून्य होता हैं । बिंदु A तथा B पर स्थित (-q) तथा (+ q) आवेश के सरल निकाय के लिए चित्र से (−q)→r1+(+q)→r2=q(→r2−→r1)=q→r=→P = व्दिध्रुव - आघूर्ण सदिश । व्यापक रुप से यदि आवेश के वितरण में नेट आवेश शून्य हो , तो उस निकाय का व्दिध्रुव - आघूर्ण सदिश रुप से परिभाषित होता हैं :
आवेश के असंतत (discrete) वितरण के लिए , →P=∑−−→riqi तथा आवेश के संतत ( continuous) वितरण के लिए , →P=∫→ridqi
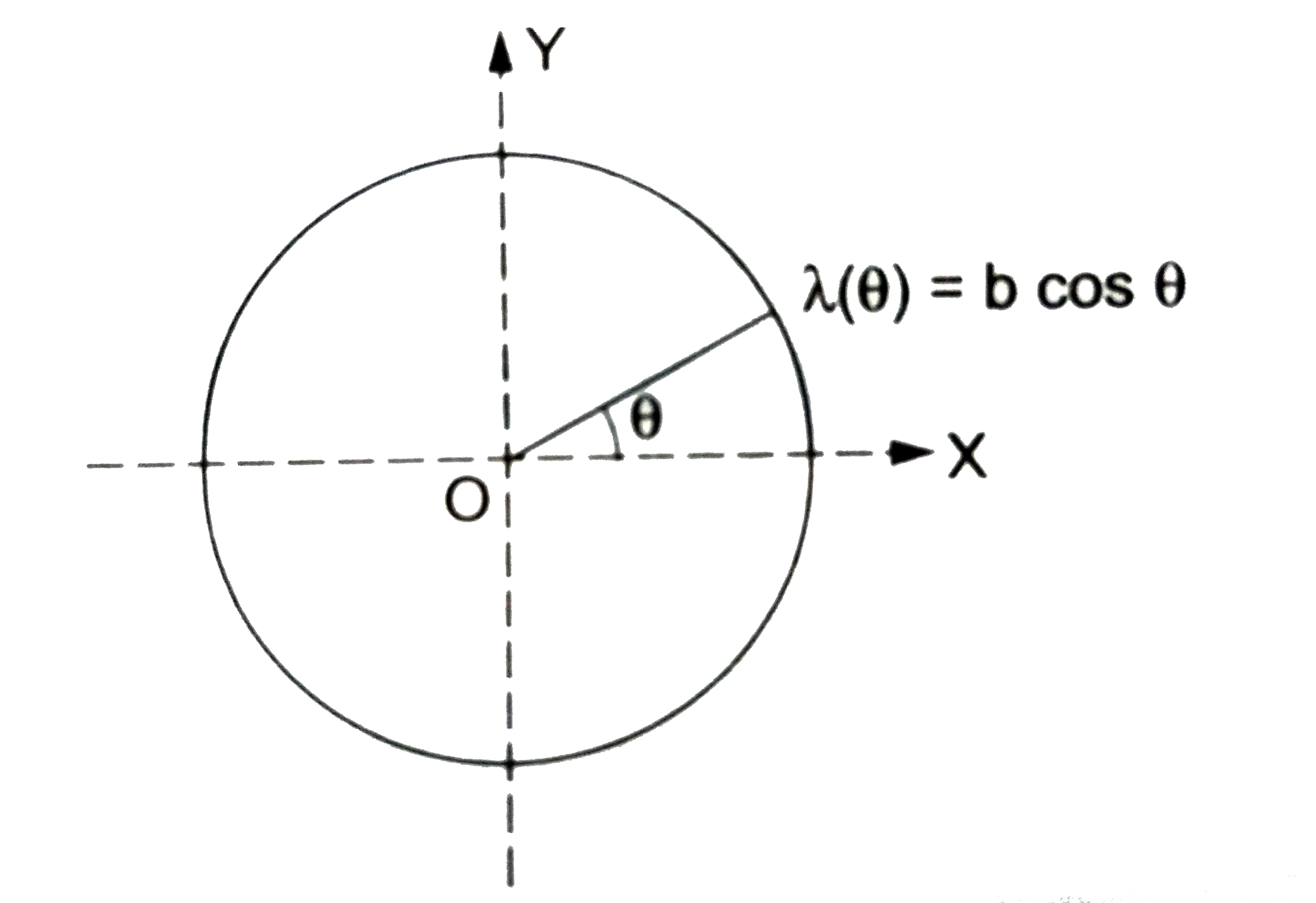
XY - तल में स्थित त्रिज्या R के एक आवेशित रिंग का केंद्र - मूलबिंदु o पर स्थित हैं तथा इसके आवेश का रैखिक घनत्व λ, कोण θ के फलन के रुप में संबंध λ(θ)=bcosθ से व्यक्त होता हैं । आवेशित रिंग का विद्युत व्दिध्रुव - आघूर्ण हैं
View Solutionयदि →a×→b=→c×→d तथा →a×→c=→b×→d, तो दिखाएँ कि (→a−→d),(→b−→c) के समान्तर है, यह दिया है कि →a≠→d तथा →b≠→c.
View Solution→a×→b तथा ∣∣→a×→b∣∣ ज्ञात करें यदि
→a=2ˆi+ˆj+3ˆk तथा →b=3ˆi+5ˆj−2ˆk
View Solution→a×→b तथा ∣∣→a×→b∣∣ ज्ञात करें यदि
→a=ˆi−7ˆj+7ˆk तथा →b=3ˆi−2ˆj+2ˆk
View Solutionयदि →a=7ˆi+3ˆj−5ˆk,→b=2ˆi+5ˆj−ˆk तथा →c=−ˆi+2ˆj+4ˆk तो (→a−→b)×(→c−→b) ज्ञात करें |
View Solutionयदि →a=2ˆi+2ˆj−ˆk, तथा →b=3ˆi−ˆj−ˆk तथा →c=ˆi+2ˆj−3ˆk, तो सत्यापित करें कि
→a×(→b×→c)=(→a⋅→c)→b−(→a⋅→b)→c.
View Solutionयदि →a=(0,1,−1) तथा →c=(1,1,1) दिए गए सदिश हैं तो एक सदिश →b ज्ञात करें जो →a×→b+→c=0 तथा →a⋅→b=3 को संतुष्ट करता है |
View Solutionमाना कि △PQR एक त्रिभुज है तथा →a=−−→QR,→b=−−→RP तथा →c=−−→PQ है | यदि |→a|=12,∣∣→b∣∣=4√3 तथा →b.→c=24 तो निम्न में से कोण-सा (से) सही है
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionमाना →a=4ˆi+5ˆj−ˆk,→b=ˆi−4ˆj+5ˆk तथा →c=3ˆi+ˆj−ˆk हैं | एक सदिश →d ज्ञात कीजिए जो →c तथा →b दोनों पर लम्ब है और →d⋅→a=21 है |
View Solutionमाना →U एक ऐसा सदिश है जो सदिशों →a=2ˆi+3ˆj−ˆk तथा →b=ˆj+ˆk के साथ समतलीय है | यदि →U,→a पर लम्बवत है तथा →U⋅→b=24 है, तो ∣∣→U∣∣2 बराबर है :
View Solutionयदि −−→BC=4→a−8→b तथा −−→AB=→a−2→b हो , तो निम्न में सही संबंध है -
View Solution

