A hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will loss half the maximum heat it can lose.
We have,
dθdt=−k(θ−θ0)
where θ0 is the temperature of the surrounding and θ is the temperature of the body at time t. Suppose θ=θ1 at t=0
Then,
∫θθ1dθθ−θ0=−k∫t0dt
or Inθ−θ0θ1−θ0=−kt
or, θ−θ0=(θ1−θ0)e−kt.........(i)
The body continues to lose heat till its temperature becomes equal to that of the surrounding. the loss of heat in this entire period is
ΔQm=msθ1−θ02
If the body loses this heat in time t1, the temperature at t1 will be
θ1−θ1−θ02=θ1+θ02
Putting these value of time and temperature in (i),
θ1+θ02−θ0=(θ1−θ0)e−kt
or, e−kt=12
or t1=In2k
Topper's Solved these Questions
Similar Questions
A hot body placed in air is cooled down according to newton's law of cooling the rate of decrease of temperature being k times the temperature difference from the surrounnding Starting from t=0 The time in which the body will lose half of the maximum heat is xLn22k Find the value of x .
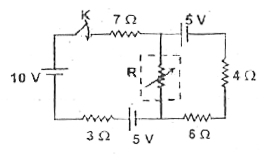
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
According to Newton’s law of cooling. The rate of loss of heat, −dθ/dtof the body is
Adirectly proportional to the sum of temperature of the body and Its surroundingsBInversely proportional to the sum of temperature of the body and Its surroundingsCdirectly proportional to the difference of temperature of the body and the surroundingsDInversely proportional to the sum of temperature of the body and the surroundings - Question 2 - Select One
Newton's law of cooling holds good provided the temperature difference between the body and the surroundings is .
AlargeBsmallCvery largeDany value - Question 3 - Select One
According to Newton's law of cooling, the body cools from 100∘C→60∘C in 20 minutes. The temperature of the surrounding being 20∘C The body cool down to 30∘C in
A40 minutesB50 minutesC90 minutesD60 minutes
Newton’s law of cooling, holds good only if the temperature difference between the body and the surroundings is
View SolutionAccording to Newton's law of cooling, the body cools from 80∘Cand50∘C at room temperature of 25∘C in 30 minutes. After 1 hours, the temperature of the body is
View SolutionAccording to Newton’s law of cooling, the rate of cooling of a body is proportional to (Δθ)n , where Δθis the difference of the temperature of the body and the surrounding, and n is equal to :
View SolutionAccording to Newton's law of cooling, the rate of cooling of a body is proportional to (Δθ)n, where Δθ is the difference of the temperature of the body and the surroundings, and n is equal to
View SolutionAccording to Newton's law of cooling, the rate of cooling of a body is proportional to (Δθ)n, where Δθ is the difference of the temperature of the body and the surroundings, and n is equal to
View Solution

