A satellite is a circular orbit radius 7000 km around the Earth. If it is transferred to circular orbit of double the radius,
Column IColumn II(A)Angular momentum(P)increase.(B)Area of Earth covered by satellite signal(Q)decreases.(C)potential energy(R)becomes double.(D)kinetic energy(S)becomes half.
The correct Answer is:A, B, C, D
(A) L=mvr=m(√GMr)r
∴L∝√r
So angular momentum increase and becomes √2 times
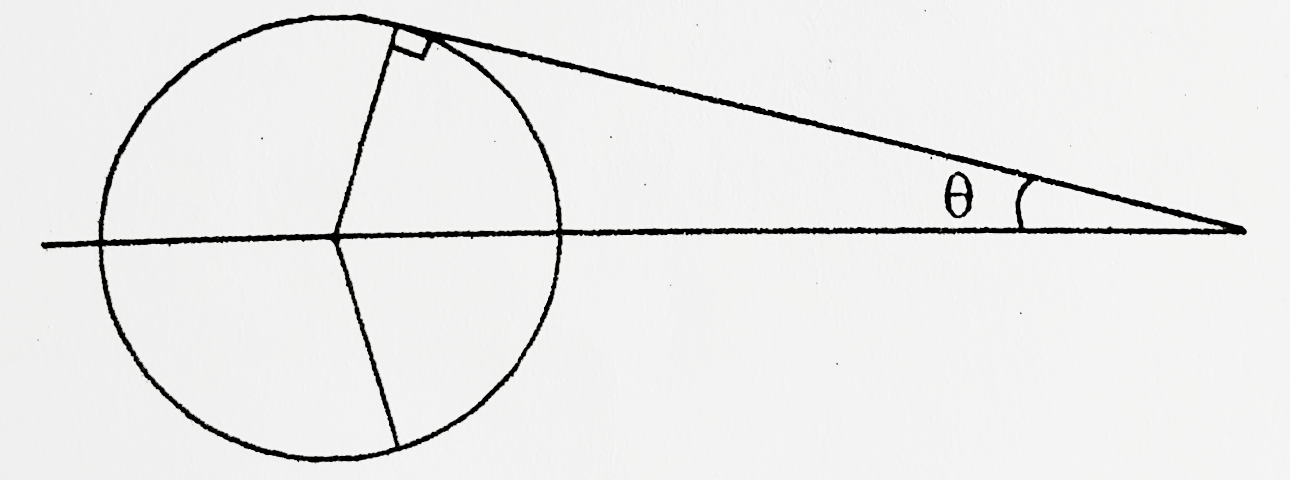
A=4πR2−2×2πR2(1−cosθ)=4πR2cosθ
So, area covered by satellite increases
(C ) U=−GMmr
So, when r is double PE becomes half and increases
KE=GMmr
So, KE decreases and becomes half
Related Playlists
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -2 [Reasoning Type]5videos
GRAVITATION
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -2 [Multiple Cprrect Choice Type]15videos
GRAVITATION
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -1 [Single Correct Choice Type]21videos
GRAVITATION
- BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)8videos
CENTRE OF MASS & MOMENTUM CONSERVATION
- BOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise89videos
HEAT TRANSFER
Similar Questions
A 400 kg satellite is in a circular orbite of radius 2R around the earth how much energy is required to transfer it to circular orbit of radius 4R
View SolutionA satellite is revolving in circular orbit of radius r around the earth of mass M. Time of revolution of satellite is
View SolutionA satellite whose mass is M , is revolving in circular orbit of radius r around the earth. Time of revolution of satellite is
View SolutionFor a satellite moving in a circular orbit around the earth, the ratio of its total mechanical energy to kinetic energy
View SolutionA satellite is launched into a circular orbit of radius R around the earth. A second satellite is launched into an orbit of radius 4R. The ratio of their respective periods is
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. then, its angular momentum will be
View SolutionA satellite of mass m moves around the Earth in a circular orbit with speed v. The potential energy of the satellite is
View SolutionA satellite is moving around the earth's with speed v in a circular orbit of radius r. If the orbit radius is decreases by 1% , its speed will
View SolutionA satellite of mass m is in a circular orbit of radius 2RE about the earth. The energy required to transfer it to a circular orbit of radius 4RE is (where ME and RE is the mass and radius of the earth respectively)
View SolutionA satellite of mass M revolving in a circular orbit of radius rs around the earth of mass M has a total energy E. then, its angular momentum will be
View Solution


