A small ball of mass is suspended with light inelastic string of length from a block of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle from equilibrium position and then released.
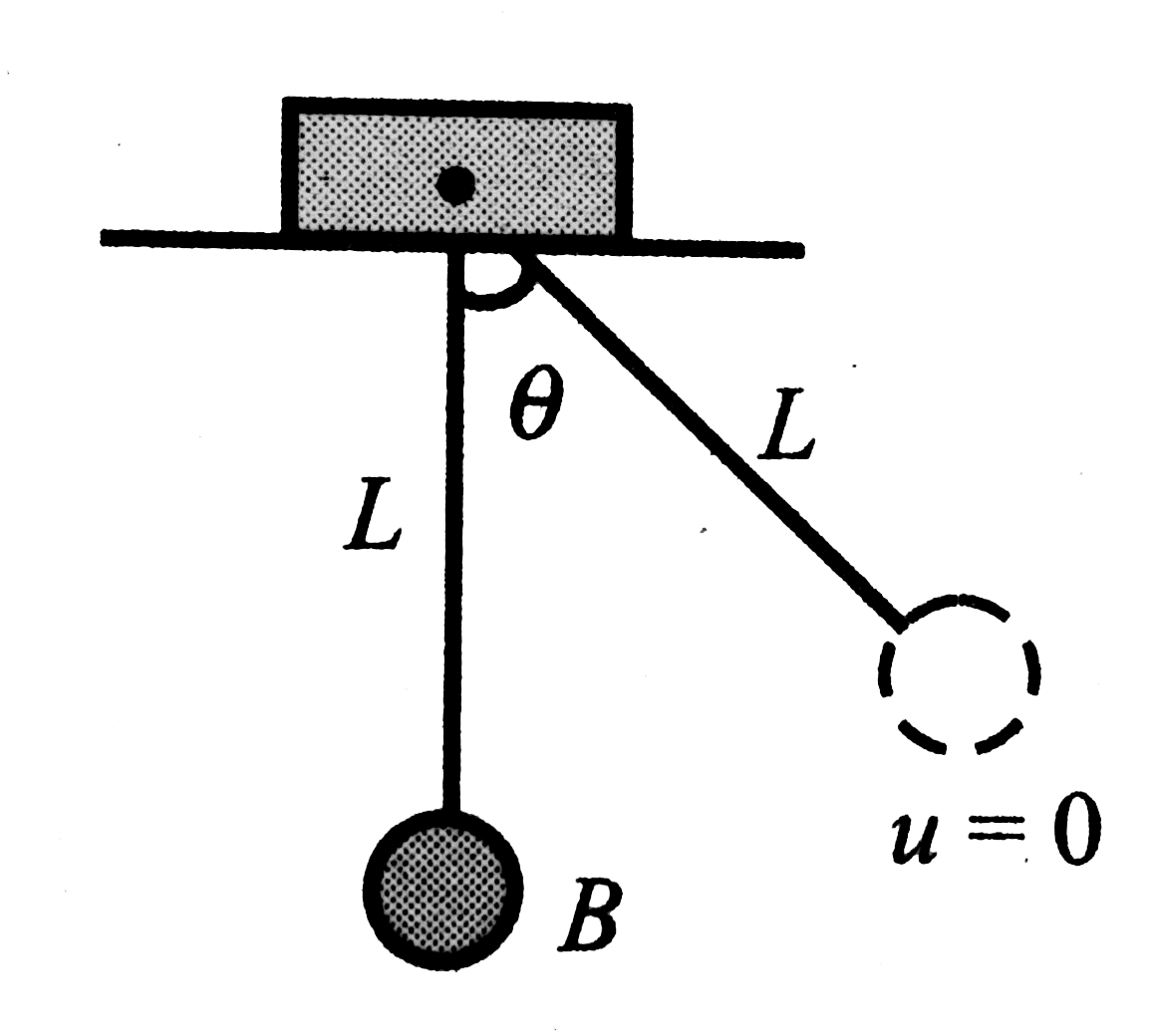 The displacement of centre of mass of system till the string becomes vertical is
The displacement of centre of mass of system till the string becomes vertical is
zero
none of these
The correct Answer is:B
(because)
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-2 [REASONING TYPE]
Explore 10 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-2 [MULTIPLE CORRECT CHOICE TYPE]
Explore 10 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
Explore 23 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
Similar Questions
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
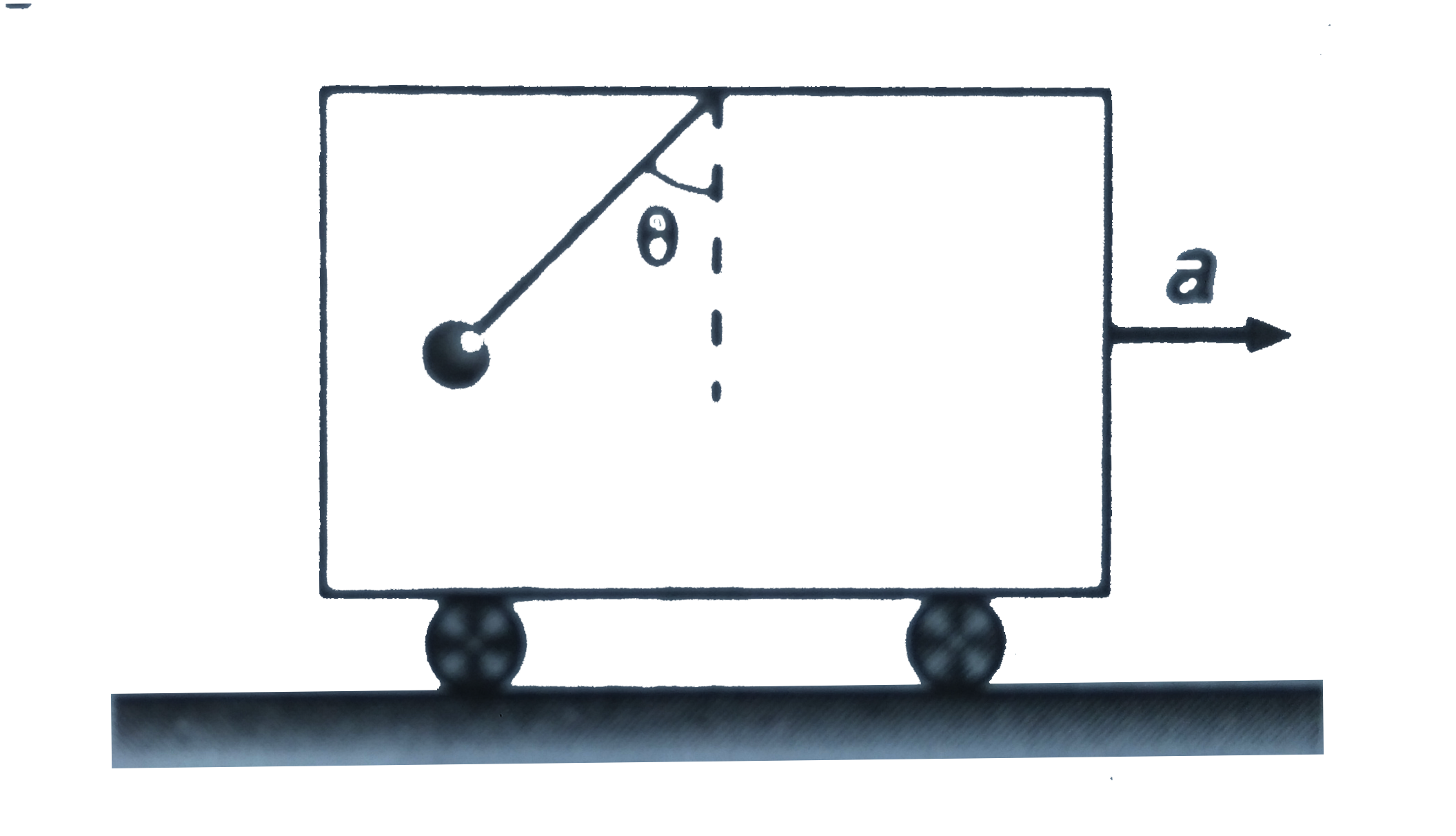
View Solution
Knowledge Check
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

The displacement of block when equilibrium position isALsinθ2BLsinθCLDnone of theseA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
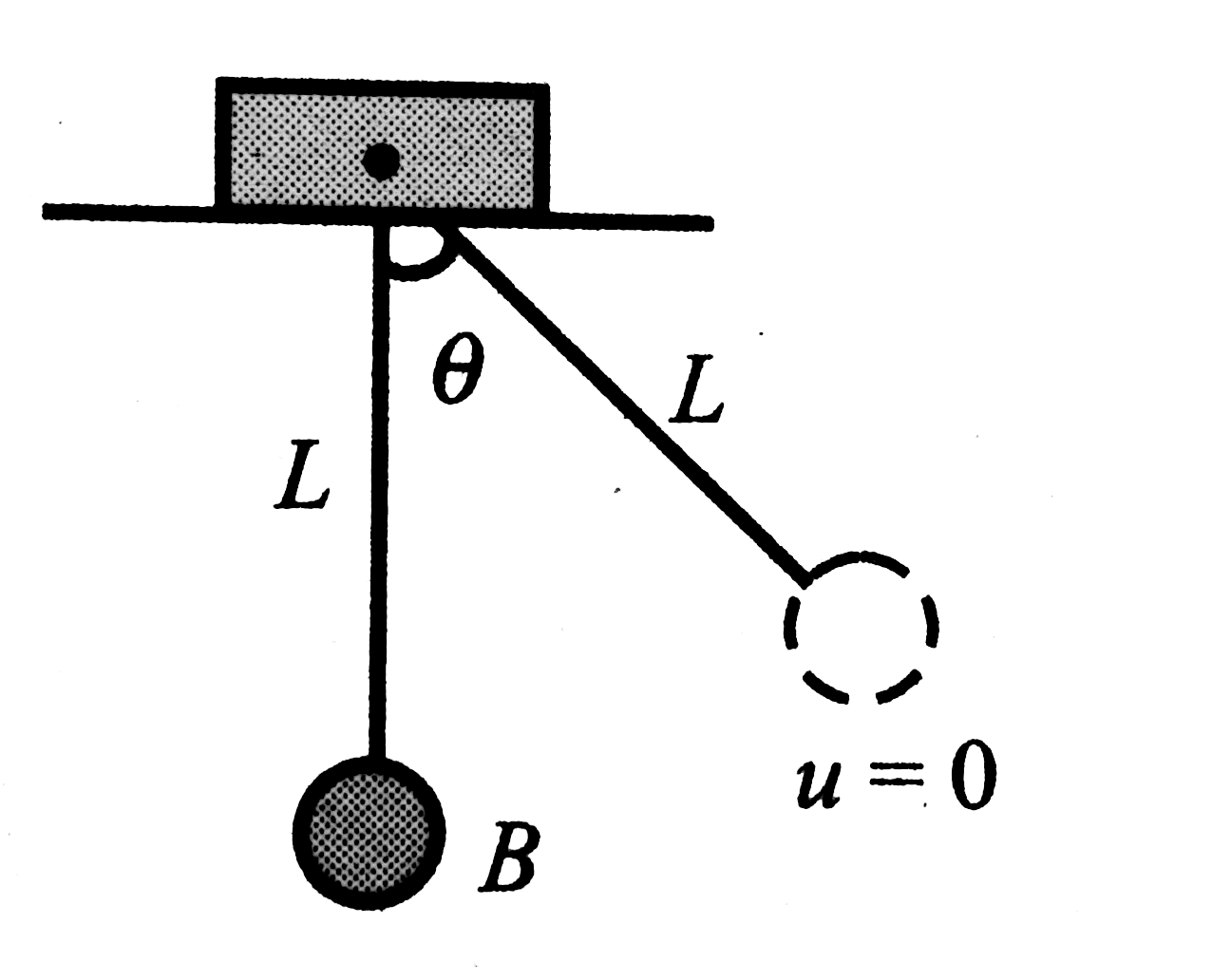
Tension in string when it is vertical, isAmgBmg(2−cosθ)Cmg(3−2cosθ)Dnone of theseA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
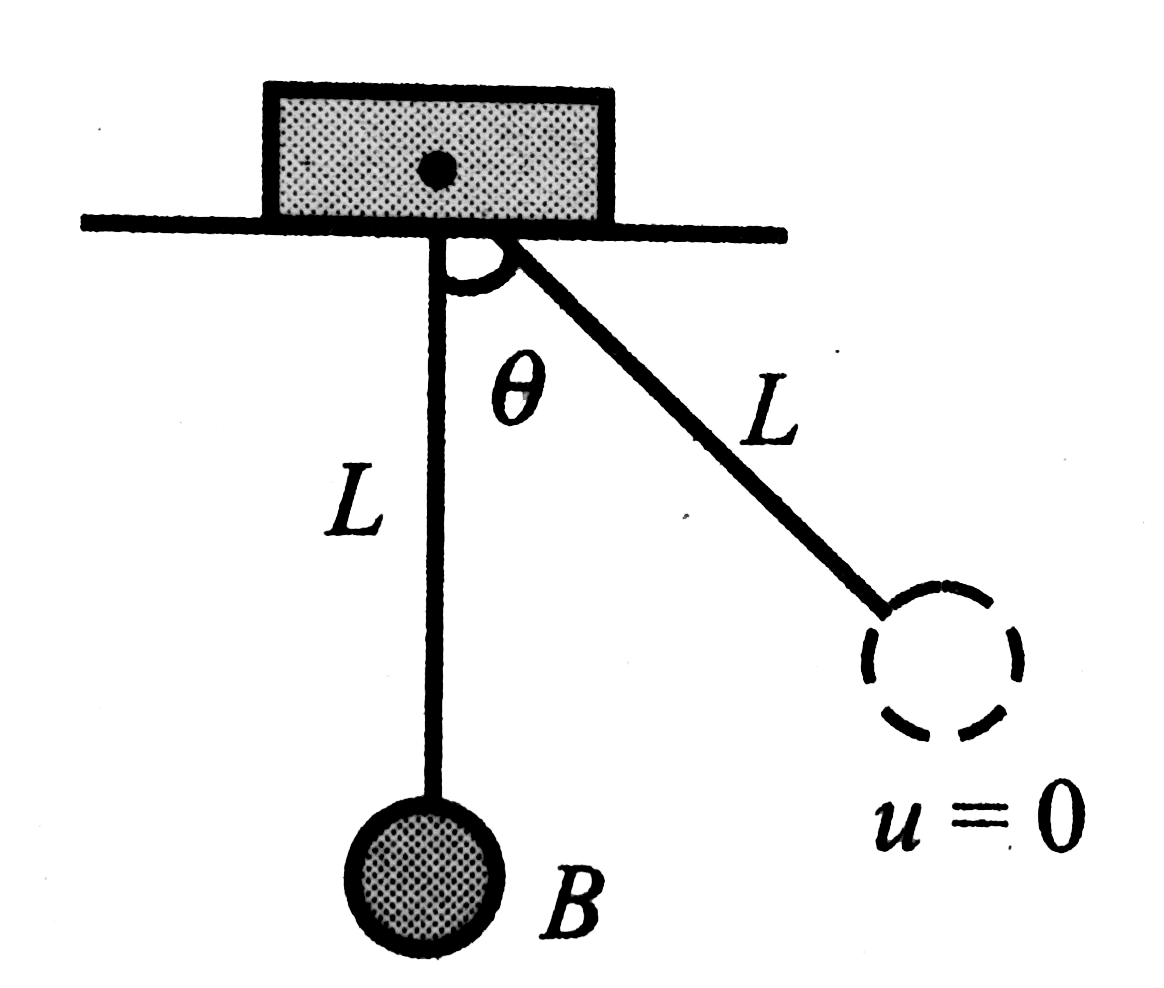
Maximum velocity of block during subsequent motion of the system after release of ball isA[gl(1−cosθ)]12B[2gl(1−cosθ)]12C[glcosθ]12Dinformation are sufficient to decide
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
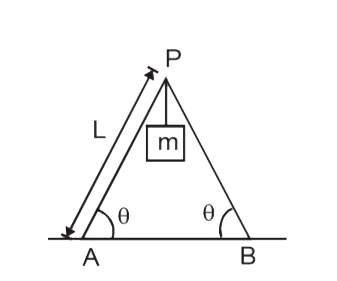
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
View SolutionA thin rod of mass M and length L is released from rest in position shown. The path of centre of mass of rod till the rod become horizontal is [ Assume surface is smooth]
_PHY_208_Q01.png)
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.

View Solution