In an organ pipe the distance between the adjacent node is 4cm. Find the frequency of source if speed of sound in air is 336m/s.
The correct Answer is:4.2kHz
λ2=4×10−2m,λ=8×10−2m
n=Vλ=3368×10−2=4200Hz=4.2KHz
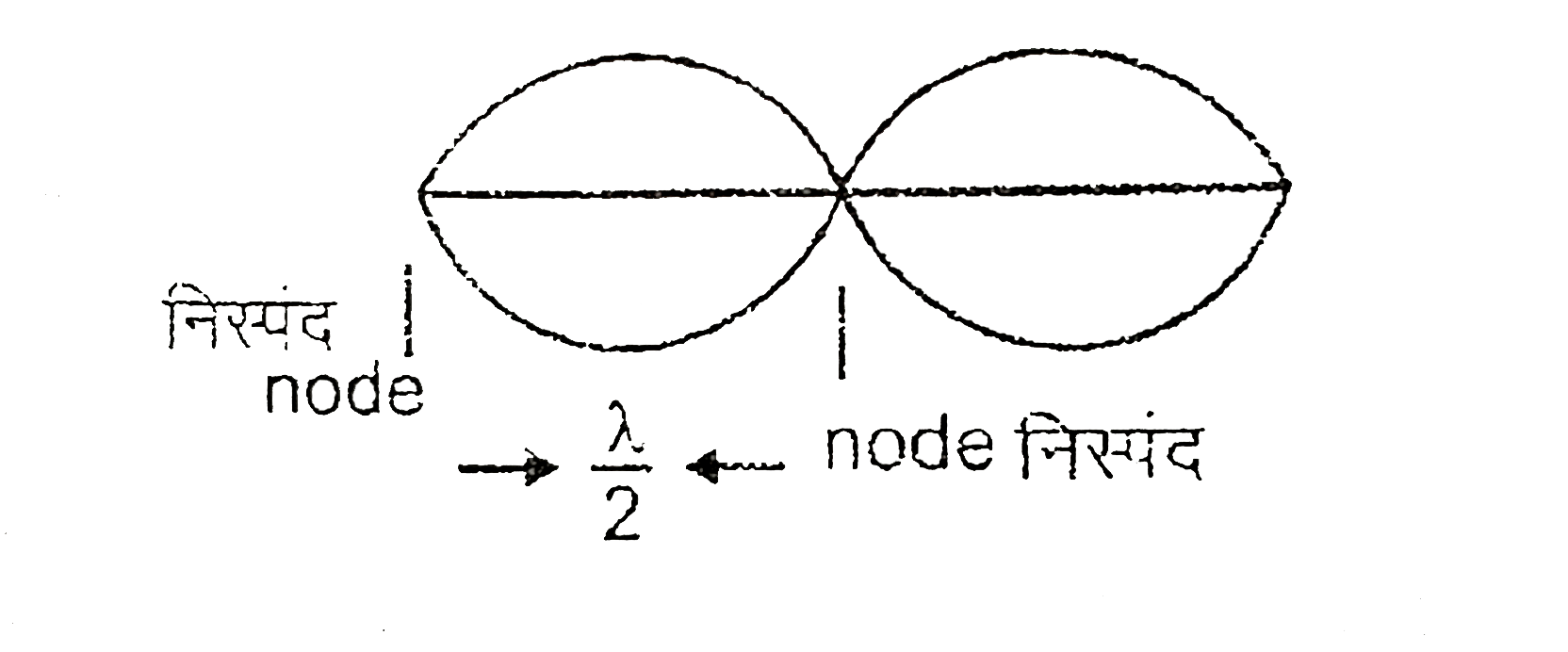
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - II
30 Videos
- SOUND WAVESBOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I
25 Videos
- SOUND WAVESBOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Board Level Exercise
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCECHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340ms−1.
View SolutionAn open organ pipe of length 1m contains a gas whose density is twice the density of atmosphere at STP. Find the difference between fundamental and second harmonic frequencies if speed of sound in atmosphere is 300 m/s.
View Solution
Knowledge Check
In an organ pipe of length L open at both ends, the fundamental mode has a frequency
(where v is a speed of sound in air)Av2L and only odd harmonies are present.Bv2L and only even harmonies are present.Cv2L and all harmonies are present.Dv4L and only odd harmonies are present.An open organ pipe sounds a fundamental note of frequency of 230 Hz . It the speed of sound in air is 330m/s ., then the length of the pipe is nearly-
A0.25mB0.50mC0.75 mD2.00mA source emitting sound of frequency 180Hz is placed in front of a wall at distance of 2m from it . A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air =360m/s.
A3mB2mC3/2mDzero
Two adjacent resonance frequency of an open organ pipe are 1800 and 2100Hz. Find the length of the tube. The speed of sound in air is 330m/s.
View SolutionFor a certain organ pipe, three successive resonance frequencies are observed at 425, 595 and 765 Hz. The speed of sound in air is 340 m/s. The pipe is
View Solution(a) A cylindrical metal tube has a length of 50cm and is open at both ends. Find the frequencies between 1000Hz and 2000Hz at which the air is 340m/s.
(b) Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20−20000Hz). Speed of sound in air =340m/s.
(c) Two successive resonance frequencies in an open organ pipe are 1944Hz and 2592Hz. Find the length of the tube. The speed of sound in air is 324m/s.
View SolutionTwo sound waves are originating from a single source. They are travelling along different paths in air before meeting at a point. If the source is vibrarting with frequency of 2 kHz and one path is 58 cm longer than the other path then discuss the nature of interference. Speed of sound in air is 336 m/s.
View SolutionA source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170ms−1. A detector is placed at a distance of 200 m from the line of motion of the source. (a) Find the frequency of sound received by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant it detects the frequency 1200 Hz. Velocity of sound in air=340ms−1.
View Solution
