The interanal radius of one limb of a capillary $U -$ tube is $r_{1} = 1 m m$ and the internal radius of the second limb is $r_{2} = 2 m m$ , the tube is filled with same mercury, and one of the limbs is connected to a vecuum pump. The surface tension & density of mercury are $480 d y n / c m$ & $13.6 g m / c m^{3}$ respectively (assume contact angle to be $θ = 180^{\circ}$ ) $(g = 9.8 m / s^{2}$ )
Which limb of the should be connected to the pump ?

A

Limb having radius $2 m m$

B

Limb having radius $1 m m$

C

Any of the limb

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Pressure difference $= \frac{2 T}{r_{1}} - \frac{2 T}{r_{2}}$ ( $∵$ angle of contact is $180^{\circ}$ )
$\Rightarrow ρ_{H g} h_{H g} \times g = 2 T (\frac{r_{2} - r_{1}}{r_{1} r_{2}})$
$\Rightarrow h_{H g} = \frac{2 T}{ρ g} (\frac{r_{2} - r_{1}}{r_{1} r_{2}}) = 3.53 m m$ of $H g$ .
As $P_{A} > P_{B}$ , althorugh they are at same height, hence the air above the point $B$ has been evacuated.
So the bigger limb of the tube should be connected to the pump.

|

Updated on:21/07/2023

Class 11 PHYSICS SURFACE TENSION

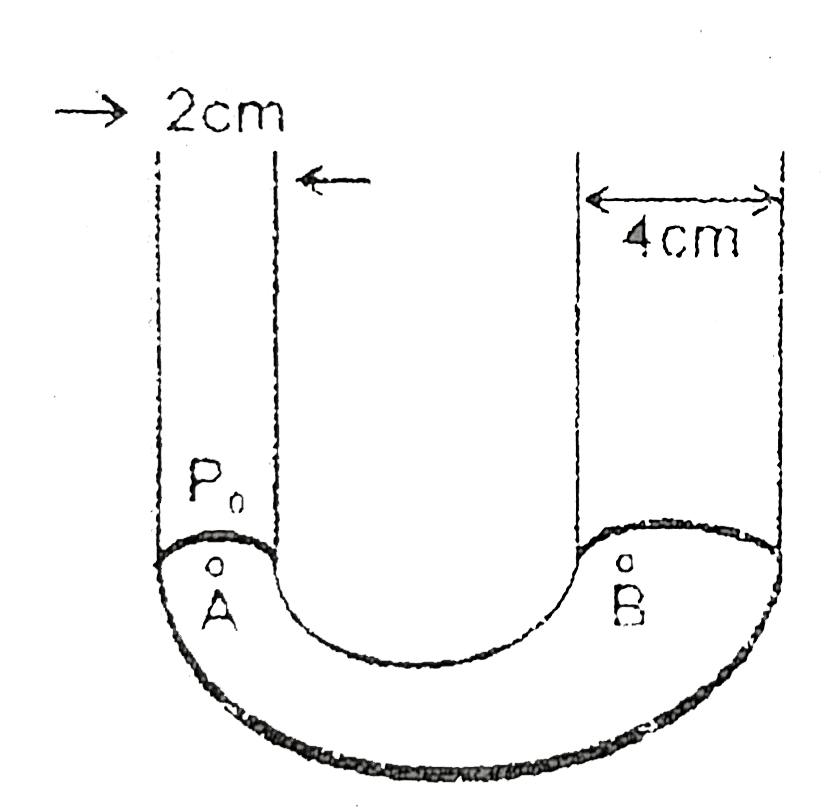
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The interanal radius of one limb of a capillary $U -$ tube is $r_{1} = 1 m m$ and the internal radius of the second limb is $r_{2} = 2 m m$ , the tube is filled with same mercury, and one of the limbs is connected to a vecuum pump. The surface tension & density of mercury are $480 dyn / cm$ & $13.6 g m / c m^{3}$ respectively (assume contact angle to be $θ = 180^{\circ}$ ) $(g = 9.8 m / s^{2}$ )
What will be the difference in air pressure when the mercury levels in both limbs are at the same height ?
A $3.53 m m$ of $H g$
B $1.51 m m$ of $H g$
C $0.51 m m$ of $H g$
D $5.52 m m$ of $H g$
Question 2 - Select One
A capillary tube is held vertically in water . The internal radius of the tube is $(1 / 42)$ cm . If the surface tension is 70 dyne /cm and angle of contact is zero , then rise in the capillary tube is
A6 cm
B4 cm
C12 cm
D24 cm
Question 3 - Select One
Water rises to a height fo 6 cm in a capillary tube of radius $r$ . If the radius of the capillary tube is 3r, the height to which water will rise is ….cm.
A18
B9
C2
D3

RESONANCE-SURFACE TENSION-Exercise- 2 PART - IV

Home
Ask Doubt
Profile