A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle θ with vertical edge of the disc. If the disc displaces a weight of water W and surface tension of water is T, then the weight of metal disc is :
2πrT+W
2πrTcosθ−W
2πrTcosθ+W
W−2πrTcosθ
The correct Answer is:C
Step by step video, text & image solution for A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle theta with vertical edge of the disc. If the disc displaces a weight of water W and surface tension of water is T, then the weight of metal disc is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SURFACE TENSIONBook:RESONANCEChapter:SURFACE TENSIONExercise:Exercise- 2 PART - I
Explore 7 Videos
- SURFACE TENSIONBook:RESONANCEChapter:SURFACE TENSIONExercise:Exercise- 2 PART - II
Explore 15 Videos
- SURFACE TENSIONBook:RESONANCEChapter:SURFACE TENSIONExercise:Exercise- 1 PART - I
Explore 10 Videos
- STRING WAVESBook:RESONANCEChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
- UNITS, DIMENSION & MEASUREMENTBook:RESONANCEChapter:UNITS, DIMENSION & MEASUREMENTExercise:Exercise
Explore 27 Videos
Similar Questions
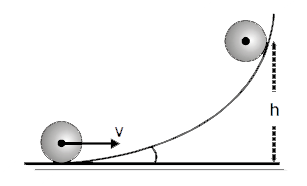
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View Solution
Knowledge Check
A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle θ with vertical edge of the disc of the disc. If the disc dispplaces a weight of water W and surface tension of water is T, then the weight of metal disc is
A2πrT+WB2πrTcosθ−WC2πrTcosθ+WDW−2πrTcosθA disc of paper of radius R is floating on the surface of water of surface tension T . If r=20 cm and T=0.070N//m , then the force of surface tension on the disc is
A2.2×10−2NB4.4×10−2NC8.8×10−2ND44×10−2NA platinum wire ring of radius 2.5 cm floats horizontally on the surface of water . A vertically force of 0.022 N is required to detach the ring from the surface of water . Then surface tension of water is
A6×10−2N/mB8×10−2N/mC7×10−2N/mD9×10−2N/m
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
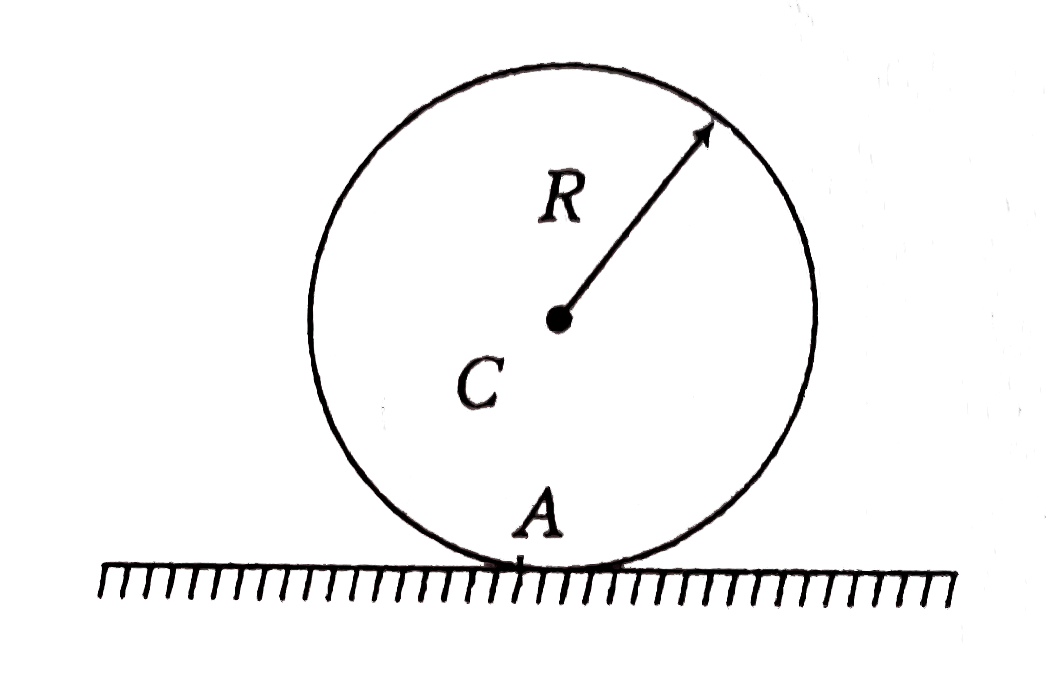
View SolutionA disc of radius R rolls on a rough horizontal surface. The distance covered by the point A in one revolution is
View SolutionThe surface tension of water is 0.07 N/m . Find the weight of water supported by surface tension in a capillary tube with a radius of 0.1 mm.
View SolutionThe length of a needle floating on water is 2.5cm. The minimum force in addition to its weight needed to lift the needle above the surface of water will be (surface tension of water is 0.072N/m)
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View Solution

