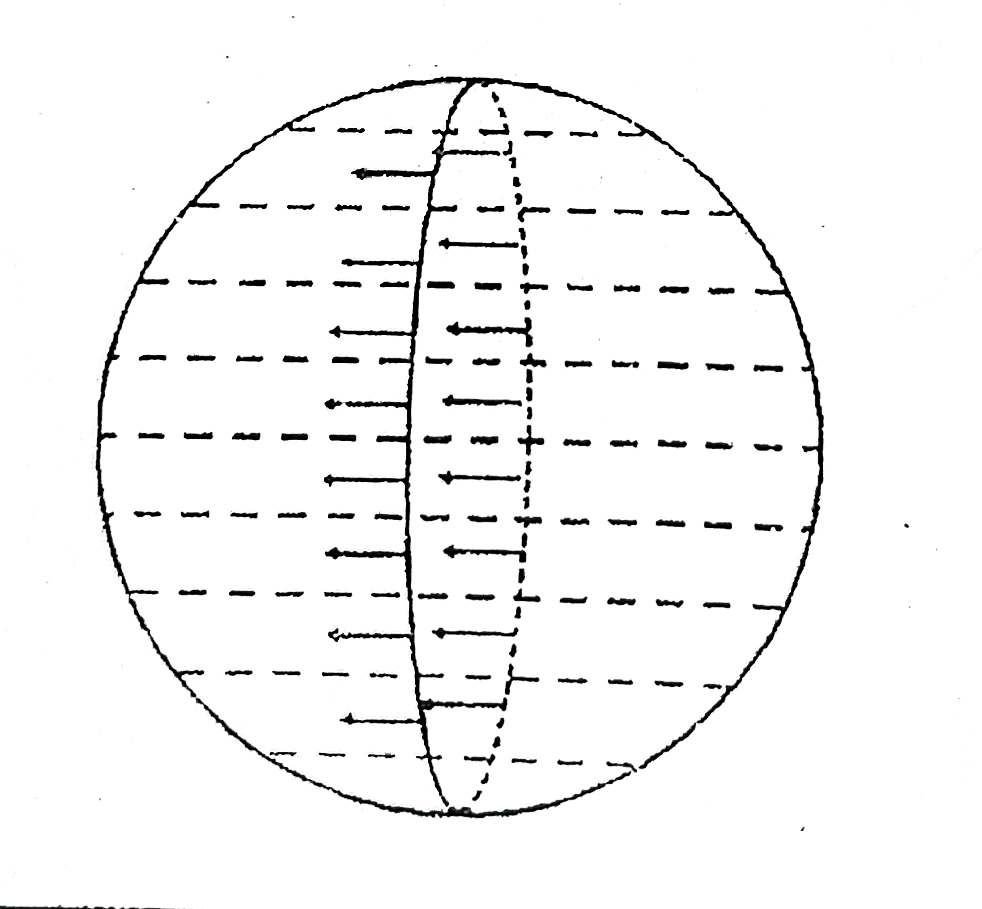
Consider the water drop of radius $R$ . Find surface tension force between the left half surface and right half surface ?

Video Solution

Text Solution

Verified by Experts

Surface tension force
$F = (T) (l)$
here $l =$ length of boundary line between left half and right half surface $= 2 π R$
So $F = (T) (2 π R)$

|

Updated on:21/07/2023

Class 11 PHYSICS SURFACE TENSION

Topper's Solved these Questions

BOOK - RESONANCECHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10videos
SURFACE TENSION
BOOK - RESONANCECHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
17videos
SURFACE TENSION
BOOK - RESONANCECHAPTER - STRING WAVESEXERCISE - Exercise
32videos
STRING WAVES
BOOK - RESONANCECHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27videos
UNITS, DIMENSION & MEASUREMENT

Similar Questions

Knowledge Check

Question 1 - Select One
The force due to surface tension is
Anormal to free surface
Bnormal to free surface downwards
Calong the free surface
Dat an angle of $60^{\circ}$ with free surface
Question 2 - Select One
Internal pressure inside a liquid drop of radius r and surface tension T is
A $\frac{2 T}{r} - P_{0}$
B $\frac{4 T}{r} + P_{0}$
C $P_{0} + \frac{2 T}{r}$
D $\frac{T}{4 r} - P_{0}$
Question 3 - Select One
The force exerted by surface tension on the free surface
Ais along the surface
Bis perpendicular to the surface directed upwards.
Cis perpendicular to the surface directed downwards.
Dnone of the above

RESONANCE-SURFACE TENSION-Advanced Level Problems

Home
Ask Doubt
Profile