Water shoots out of a pipe and nozzle as shown in the figure. The cross-sectional area for the tube at point A is four times that of the nozzle. The pressure of water at point A is 41×103Nm−2 (guage). If the height 'h' above the nozzle to which water jet will shoot is x/10 meter than x is. (Neglect all the losses occurred in the above process) [g=10m/s2]
![Water shoots out of a pipe and nozzle as shown in the figure. The cross-sectional area for the tube at point A is four times that of the nozzle. The pressure of water at point A is 41 xx 10^(3)Nm^(-2) (guage). If the height 'h' above the nozzle to which water jet will shoot is x//10 meter than x is. (Neglect all the losses occurred in the above process) [g = 10 m//s^(2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_WFPM_PHY_XI_C01_E01_079_Q01.png)
The correct Answer is:32
Step by step video, text & image solution for Water shoots out of a pipe and nozzle as shown in the figure. The cross-sectional area for the tube at point A is four times that of the nozzle. The pressure of water at point A is 41 xx 10^(3)Nm^(-2) (guage). If the height 'h' above the nozzle to which water jet will shoot is x//10 meter than x is. (Neglect all the losses occurred in the above process) [g = 10 m//s^(2)] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - III
8 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - IV
10 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - I
18 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
The cross-sectional area of water pipe entering the basement is 4cm−2 . The pressure at the point is 3.5×105Nm−2 and the speed of water is 2.2ms−1 . This pipe tapers to a cross-sectional area of 2cm2 when it reaches the second floor 10 m above . Calculate the speed and pressure at the second floor. use g=10m/s2.
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
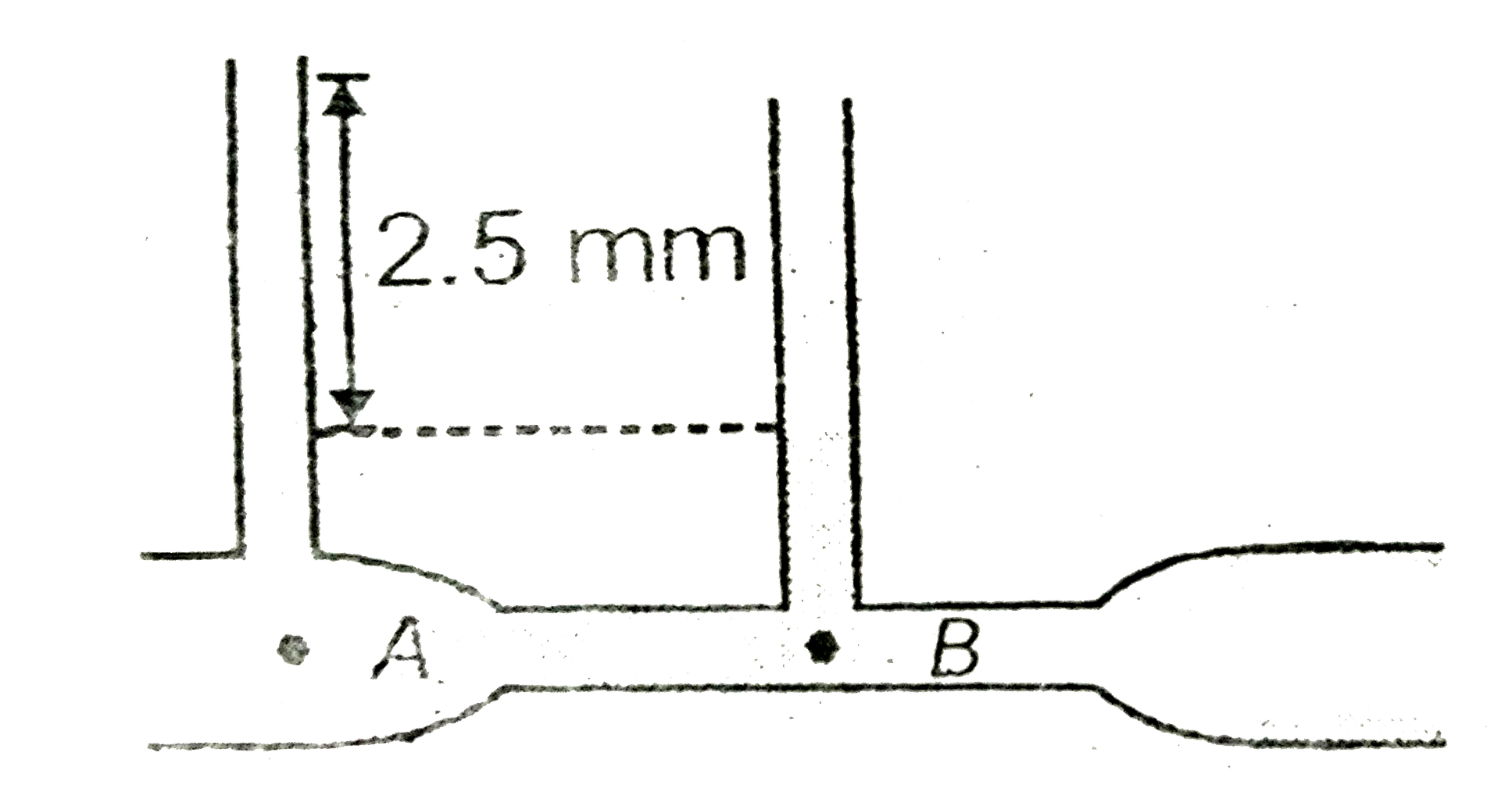
View Solution
Knowledge Check
The pressure of water in a pipe when tap is closed is 5.5×105Nm−2. The velocity with which water comes out on opening the tap is
A10ms−1B5ms−1C20ms−1D15ms−1Water is flowing through a horizontal tube having crosssectional areas of its two ends being A and A' such that the ratio All' is 5. If the pressure difference of water between the two ends is 3×105Nm−2 the velocity of water with which it enters the tube will be (neglect gravity effects)
A5ms−1B10ms−1C25ms−1D50√10ms−1Water rises to a height of 10cm in a glass capillary tube. If the area of cross section of the tube is reduced to one fourth of the former value what is the height of water rise now?
A20 cmB5 cmC2.5 cmD7 cm
The corss-sectional area of water pipe entering the basement is 4 x 10−4m2. The pressure at this point is 3 x 105Nm−2 and the speed of water is 2 ms−1. This pipe tapers to a cross-sectional area of 2 x 10−4m2 when it reaches the second flooe.
View SolutionA leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was 5×105N/m2. If the density of water is 1000kg/m3 the initial velocity with which water gushes out is approximately
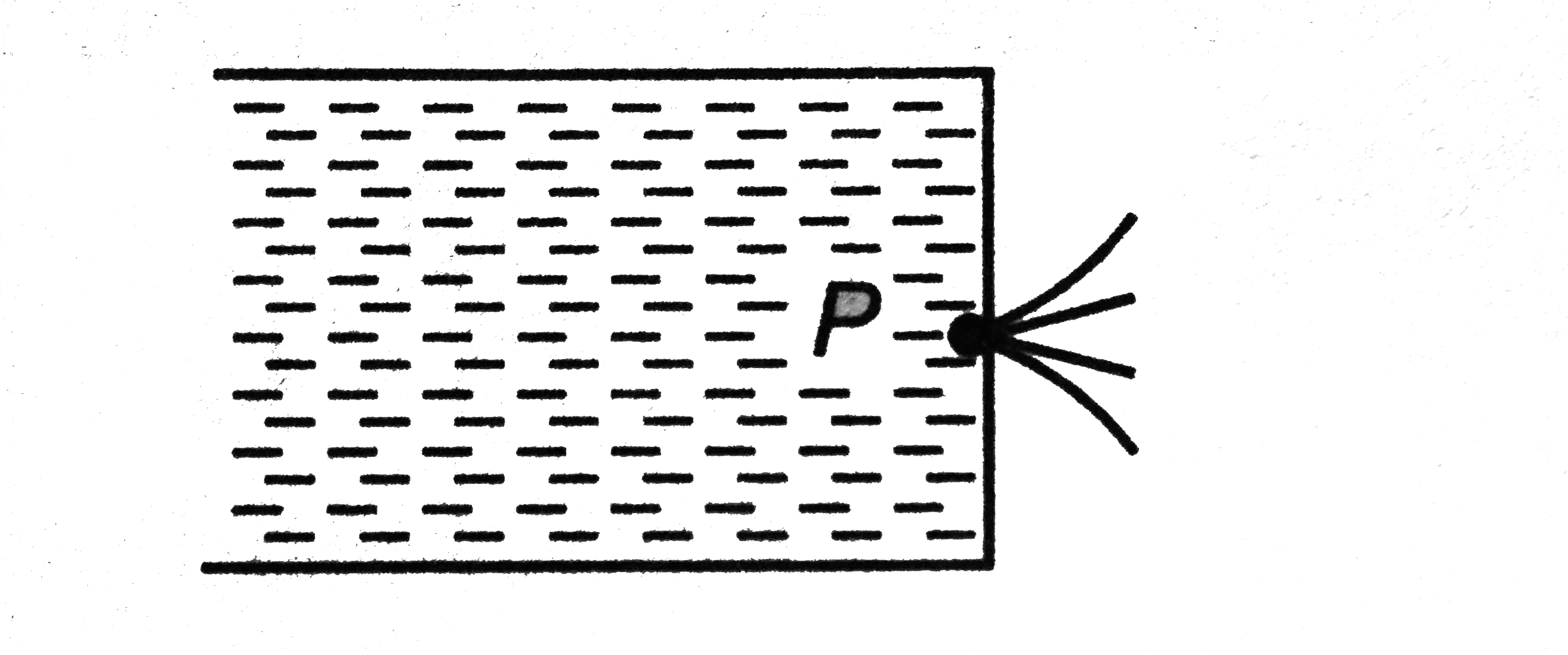
View SolutionWater is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is :
View SolutionWater is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is :
View SolutionWater is flowing through a pipe of constant cross-section. At some point the pipe becomes narrow and the cross-section is halved. The speed of water is
View Solution
