The wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
The force acting on the plank are shown in the figure. The height of water level is l. The length of the plank is 2l. The weight of the plank acts through the centre B of the plank.
We have OB=l. The buoyant force F acts though the point A which is the middle point of the dippeed part OC of the plank. We have OA=OC2=l2cosθ
Let the mass per unit length of the plank be ρ.
Its weight mg=2lρg.
The mass of the part OC of the plank =(lcosθ)ρ.
The mass of water displaced =10.5lcosθρ=2lρcosθ
The buoyant force F is, therefore, F=2lρgcosθ.
Now, for equilibrium, the torque of mg about O should balance the torque of F about O.
So, mg(OB)sinθ=F(OA)sinθ
or, (2lρ)l=(2lρcosθ)(l2cosθ) or, cos2θ=12 or, cosθ=1√2
or, θ=45∘.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise
18 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (A)
5 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Advanced Level Problems
8 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
A wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
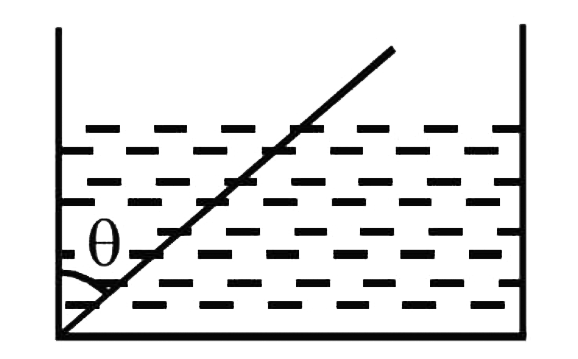
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end of the bottom of tank as shown in figure. The tank is filled with water upto a height of 0.5m. Find the angle θ that the plank makes with the vertical in the equilibrium position. [Exclude the case thea=0]

View Solution
Knowledge Check
A wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
A20cmB40cmC60cmD75cmA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
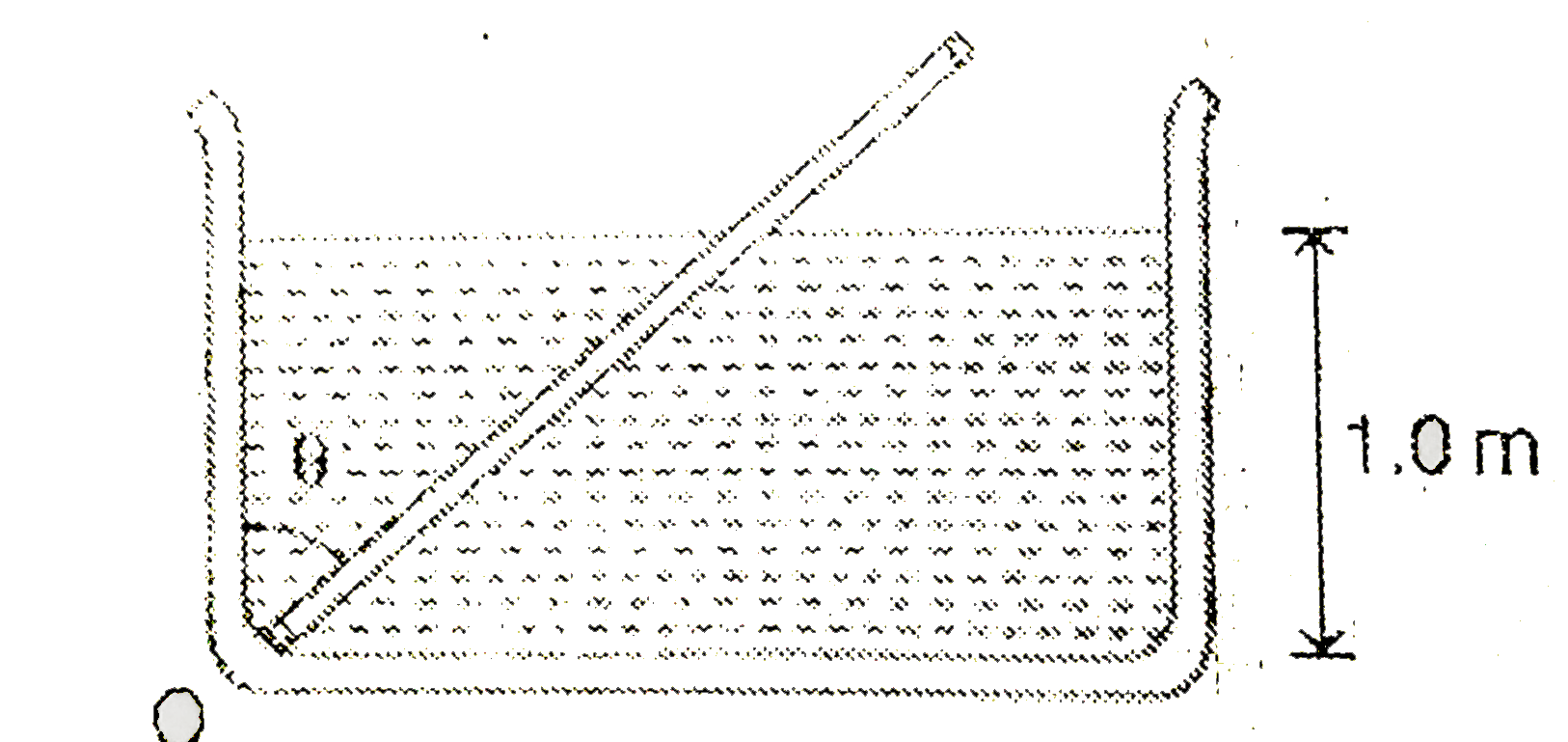 A10.2 N upwardsB4.2 N downwardsC8.3 N downwardsD6.2 N upwards
A10.2 N upwardsB4.2 N downwardsC8.3 N downwardsD6.2 N upwardsA tank 5 m high is half filled with water and then is filled to the top with oil of density 0.85 g The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2
A tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
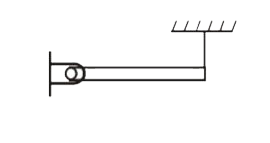
View SolutionA thin plank of mass m and length l is pivoted at one end and it is held stationary in horizontal position by means of a light thread as shown in the figure then find out the force on the pivot.
View SolutionA 50 -kg plank of length 6 m rests on the ground at one end on a frictionless roller on the top of a wall of height h=3 m at the other end. The plank projects a little beyond the wall. It remains in equilibrium for any value θ≥70∘ , where θ is the angle made by the plank with the horizontal. Find the cofficient of friction between the plank and the ground.
[Hints : Apply the equilibrium conditon that ∑→τ=0and ∑→f=0.]
View SolutionA box of mass 4 kg is placed on a wooden plank of length 1.5m which is lying on the ground. The plank is lifted from one end along its length so that it becomes inclined. It is noted that when the vertical height of the top end of the plank from the ground becomes 0.5m, the box begins to slide. Find the coefficient of friction between the box and the plank.
View SolutionA large tank is filled with water to a depth of 15 m . A spout located 10.0 m above the bottom of the tank is then opened as shown in the figure . With what speed will water emerge from the spout ?
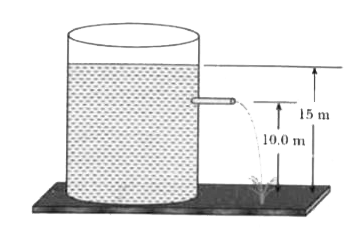
View Solution
