A pipe of diameter is connected to a water tank of large cross-sectional area in which water is maintained at a height as shown in the figure. A nozzle of diameter fitted at the end of the pipe discharges water into the atmosphere. Find the flow rate, given that the density of water is . Also find pressure at point . ( is the atmosoheric pressure)

Taking the nozzle axis as the datum and applying Bernoulli's equation
Flow rate,
Now,
Applying Bernoulli's equation at the water surface and at point
Topper's Solved these Questions
Similar Questions
A pipe having an internal diameter D is connected to another pipe of same size. Water flows into the second pipe through n holes, each of diameter d. if the water in the first pipe has speed v, the speed of water leaving the second pipe is
View SolutionA small air bubble of radius r in water is at depth h below the water surface. If P0 is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
View Solution
Knowledge Check
A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceA∣∣2P0Rh+πR2ρgh−2RT∣∣B∣∣2P0Rh+Rρgh2−2RT∣∣C∣∣P0πR2+Rρgh2−2RT∣∣D∣∣P0πR2+Rρgh2−2RT∣∣Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of the water is p at a point , where the speed of the flow is v. What is the pressure at another point , where the speed of the flow is 2 v ? Let the density of water be 1gcm−3.
Ap+(32)ρv2Bp−2ρv2Cp−3ρv2Dp−(32)ρv2The figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)

Which of the following equation expresses the fact that the flow rate at the tap is the same as at the stream point with diameter D and velocity v (i.e. D in terms of D0,v0 and v will be) :AD=D0v0vBD=D0v20v2CD=D0vv0DD=D0√v0v
The figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)
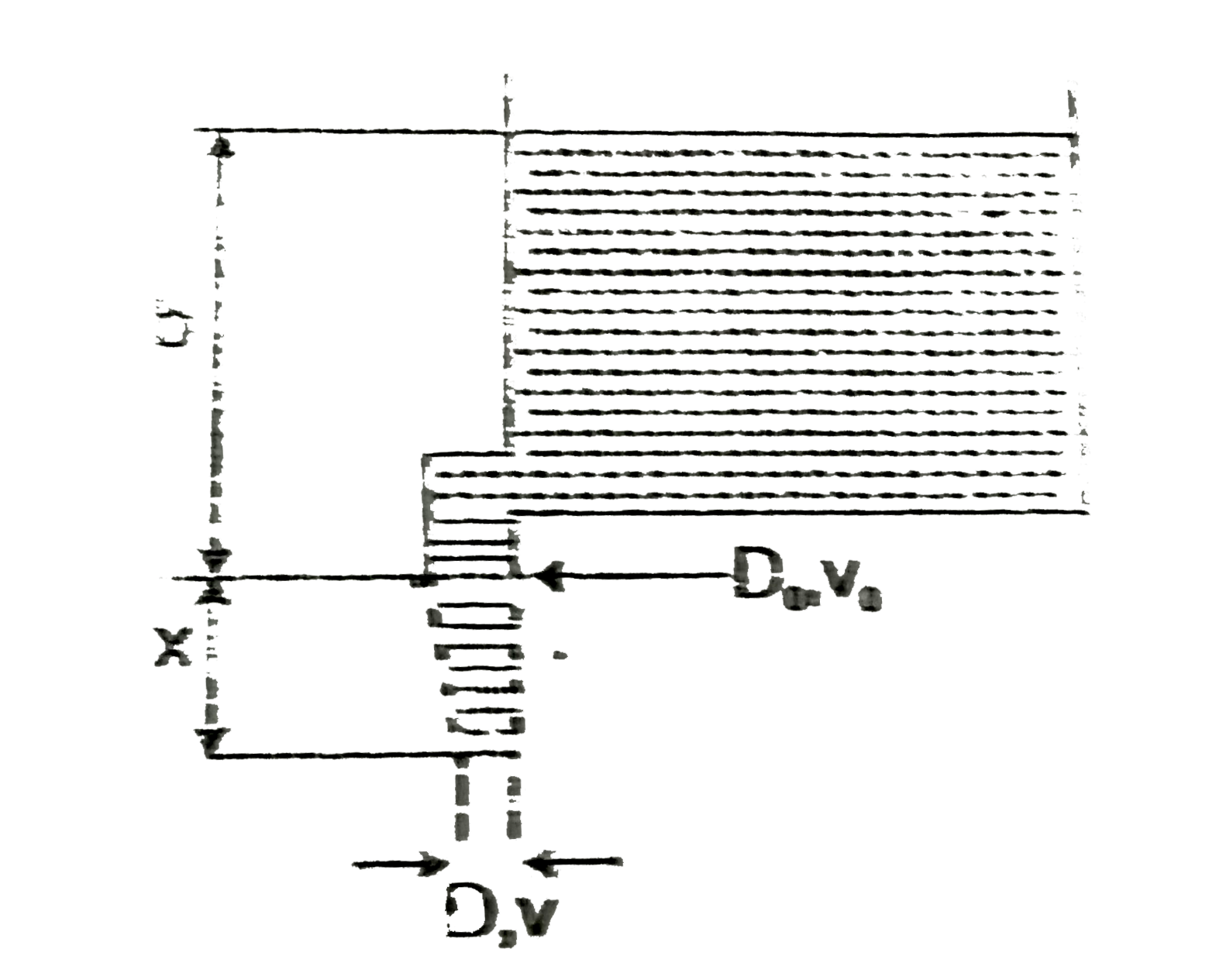
The equation for the water speed v as a funcation of the distance x below the tap will be:
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)

Equation for the stream diameter D in terms of x and D0 will be :
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)
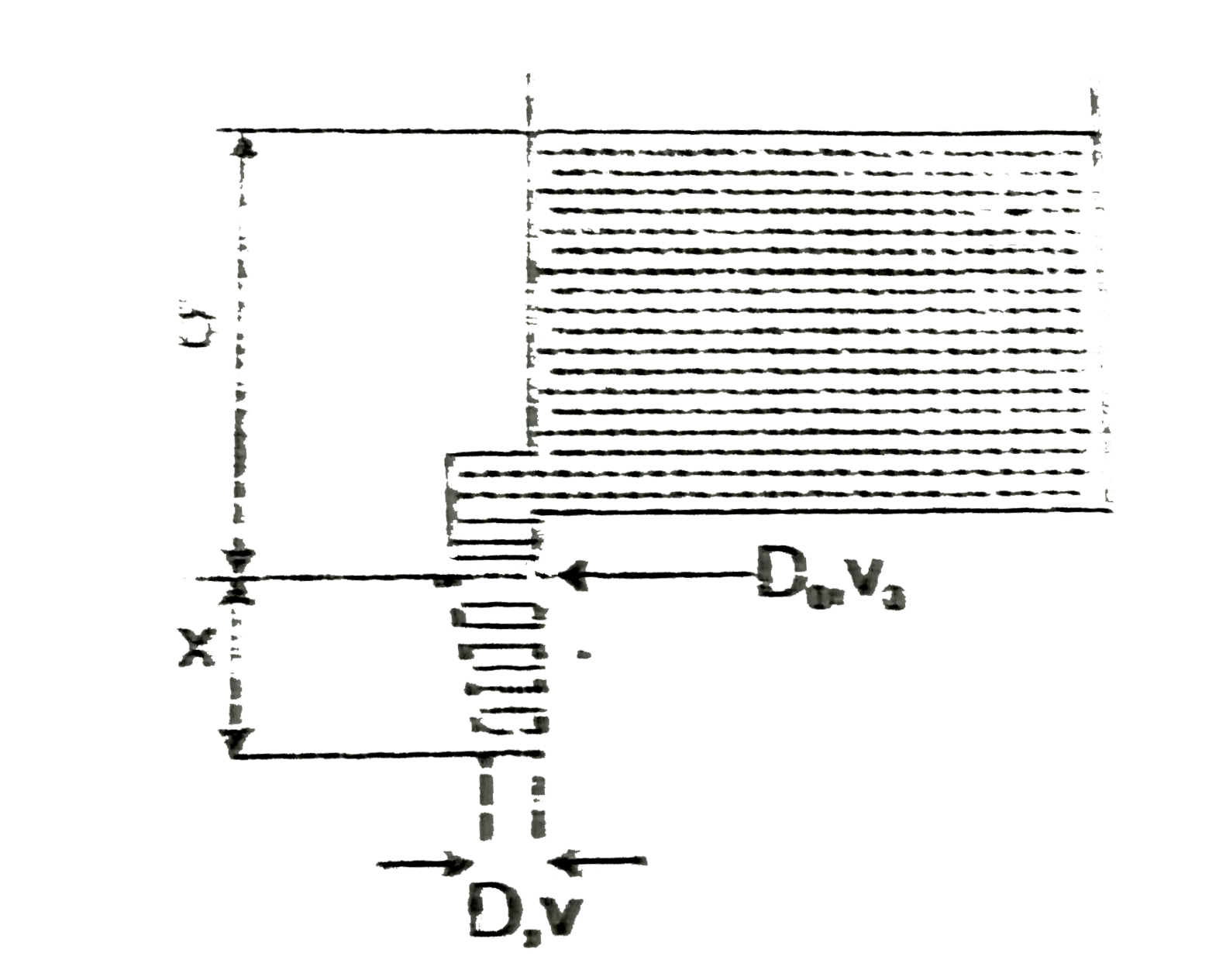
A student observes after setting up this experiment that for a tap with D0=1cm at x=0.3m the stream diameter D=0.9cm. The heights b of the water above the tap in this case will be:
View SolutionThe figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)

Equation for the flow rate, i.e. the mass of water flowing through a given point in the stream per unit time, as funcation of the water speed v will be
View SolutionWater flows steadily through a horizontal pipe of a variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, what is the pressure at another point where the velocity of flow is 2v, ρ being the density of water?
View Solution
