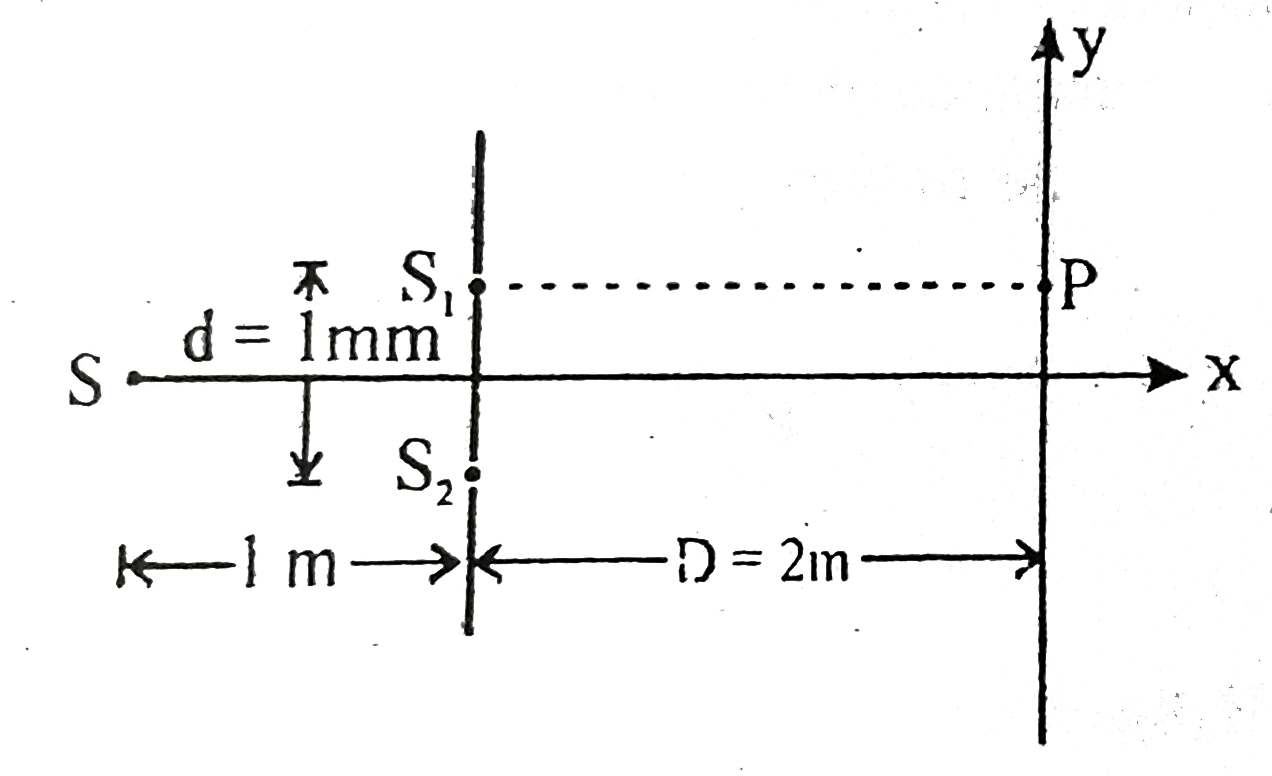
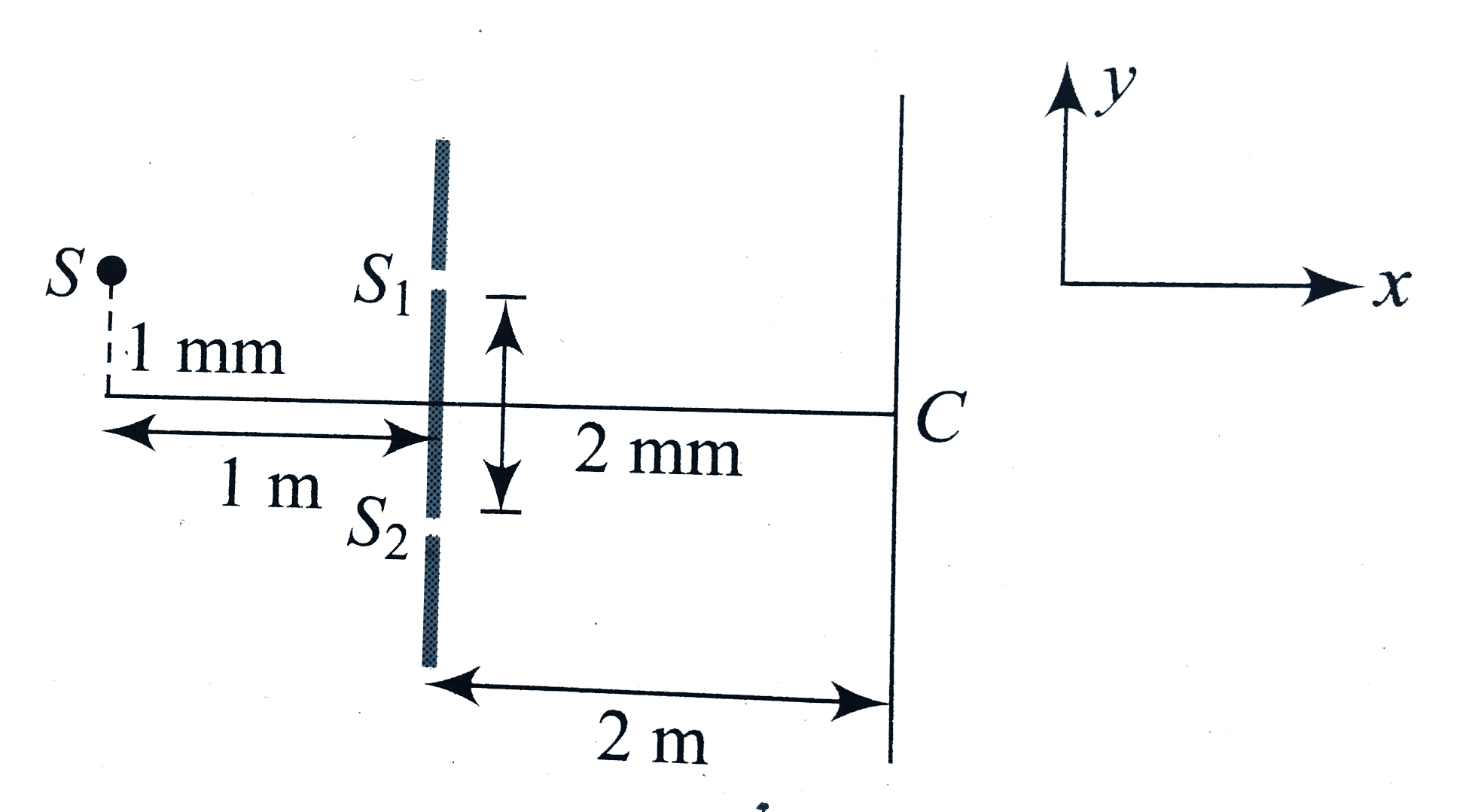
In a modified YDSE the sources S of wavelength 5000 A oscillates about axis of setup according to the equation y=0.5sin(π6)t where y is in millimeter and t in second. At what time ti will the intensity at P, a point exactly in front of slit S1 be maximum for the first time?
The correct Answer is:0001
The path difference at point P,
Δx=(SS2−SS1)+(S2P−S1P)
=dyD1+d(d/2)D2
For constructive interference,
Δx=dyD1+d22D2=nλ
(10−3)(0.5sinπt)×10−31+(10−3)22×2=nλ
(0.5sin(π6)t)×10−6+0.25×10−6
=(5000×10−10)n=0.5×10−6n
sin(π6)t=0.5n−0.250.5
For the minimum value of t n=1
sin(π6)t=12⇒(π6)t=π6ort=1sec
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Multiple objective
Explore 131 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A body oscillates with SHM according to the equation
x(t)=5cos(2πt+π/4)
where t is in second and x in metres. Calculate (a) displacement at t=0 (b) time period (c) initial velocity
View SolutionThe voltage of an ac source varies with time according to the equation V=100sin100 pi tcos100 pi t where t is in seconds and V is in volts.Then
View Solution
Knowledge Check
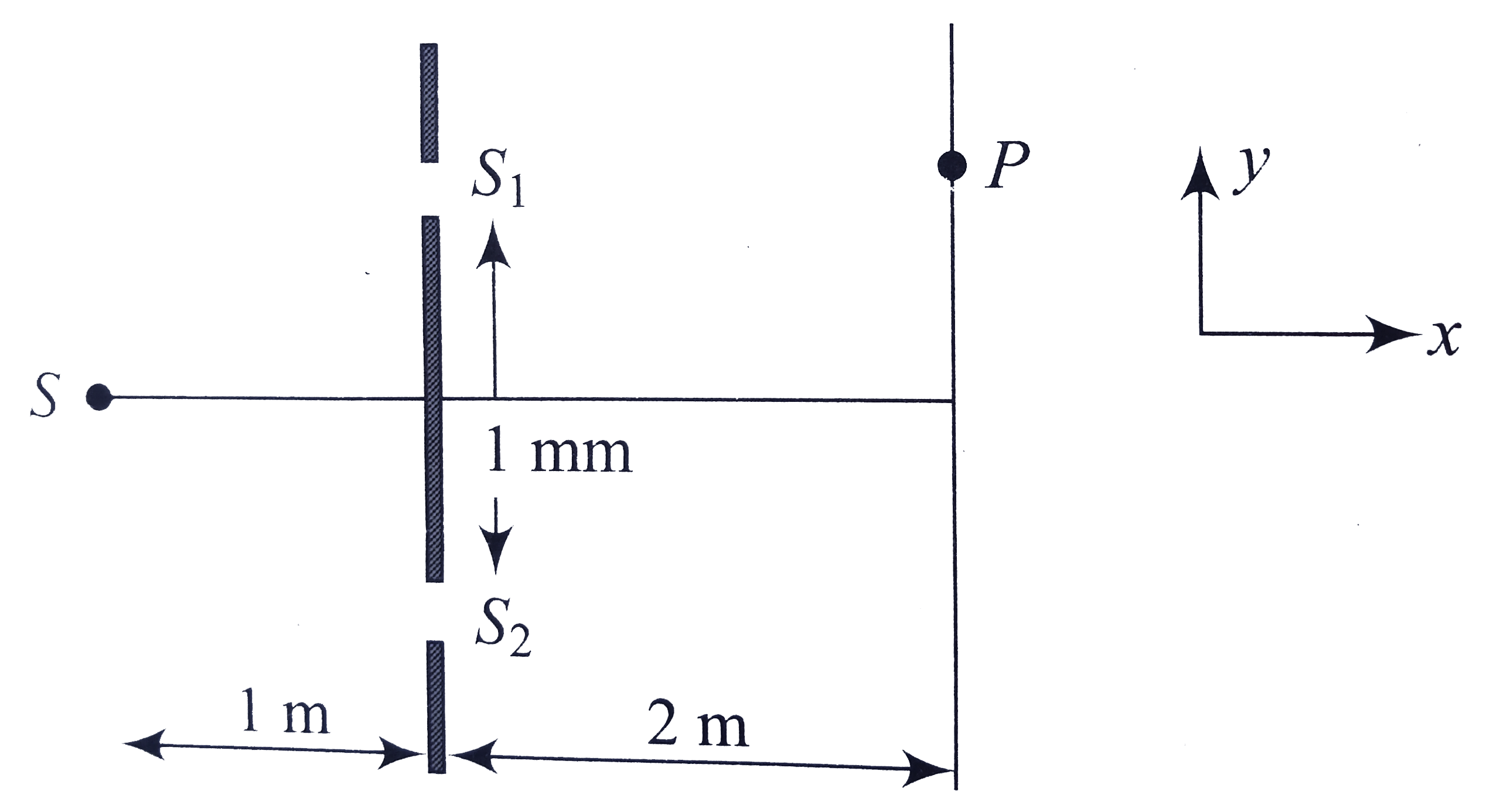
In young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits S1 and S2 which act as two coherent sources. The sources S oscillates about its own position according to the equation y=0.5sinπt, where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
 A1 sB2 sC3 sD1.5 s
A1 sB2 sC3 sD1.5 sFigure shows a Young's double slit experiment set-up. The source S of wavelength 4000Å oscillates along y-axis according to the equation y−sinπt, where y is in millimeters and t is in seconds. The distance two slits S1andS2 is 0.5 mm.
 AThe position of central maxima as a function of time is 4sinπtBThe position of central maxima as a function of time is −4sinπtCThe instant at which maximum intensity occurs at P for the first time is 1πsin−1(5980)DThe instant at which minimum intensity occurs at P for the first time is 1πsin−1(2780)
AThe position of central maxima as a function of time is 4sinπtBThe position of central maxima as a function of time is −4sinπtCThe instant at which maximum intensity occurs at P for the first time is 1πsin−1(5980)DThe instant at which minimum intensity occurs at P for the first time is 1πsin−1(2780)In a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
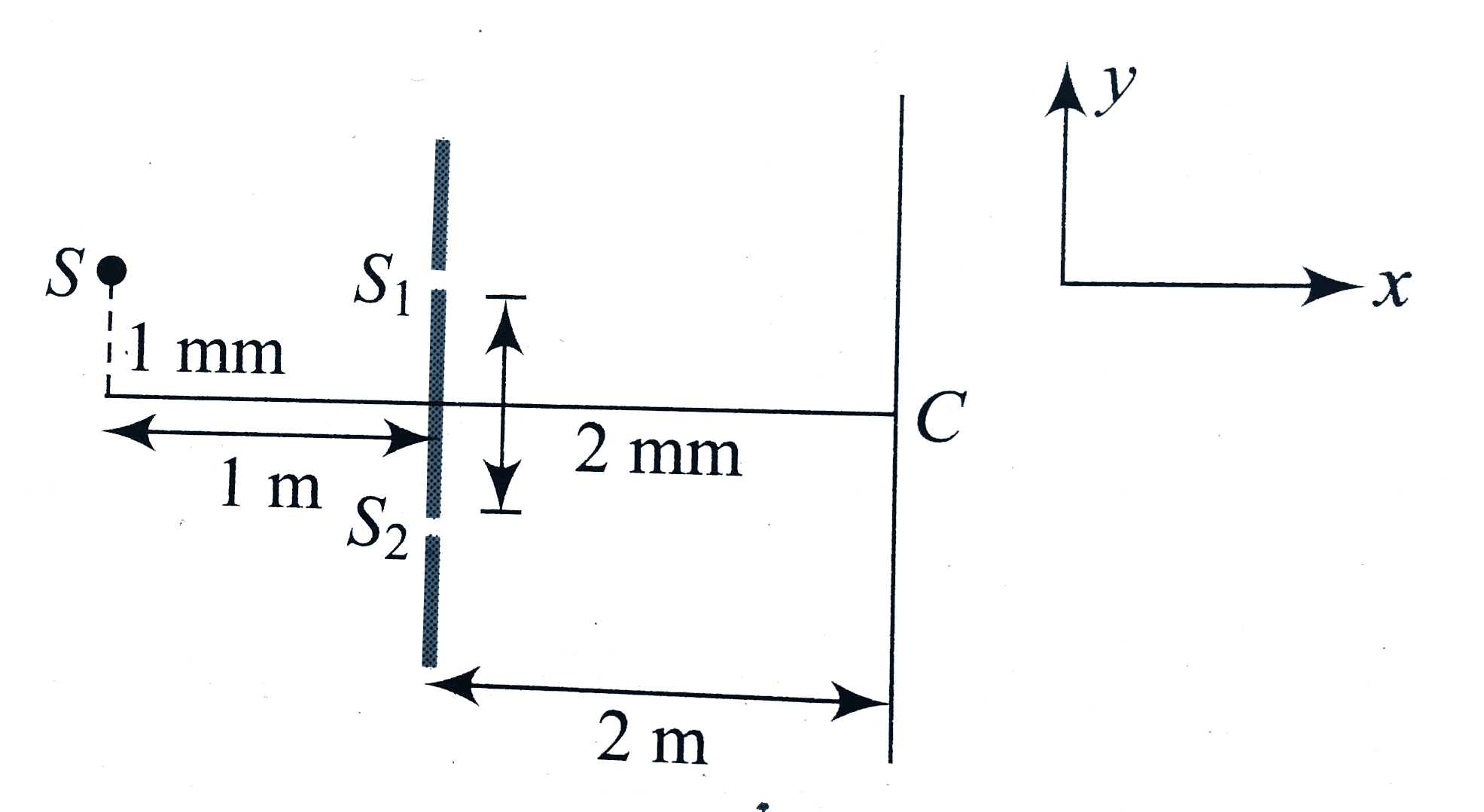
At t=1 s, a slab of thickness 2×10−3mm an refractive index 1.5 is placed just in front of S1. The central maximum is formed atA1 mm above CB1 mm below CC2 mm above CD2 mm below C
In a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
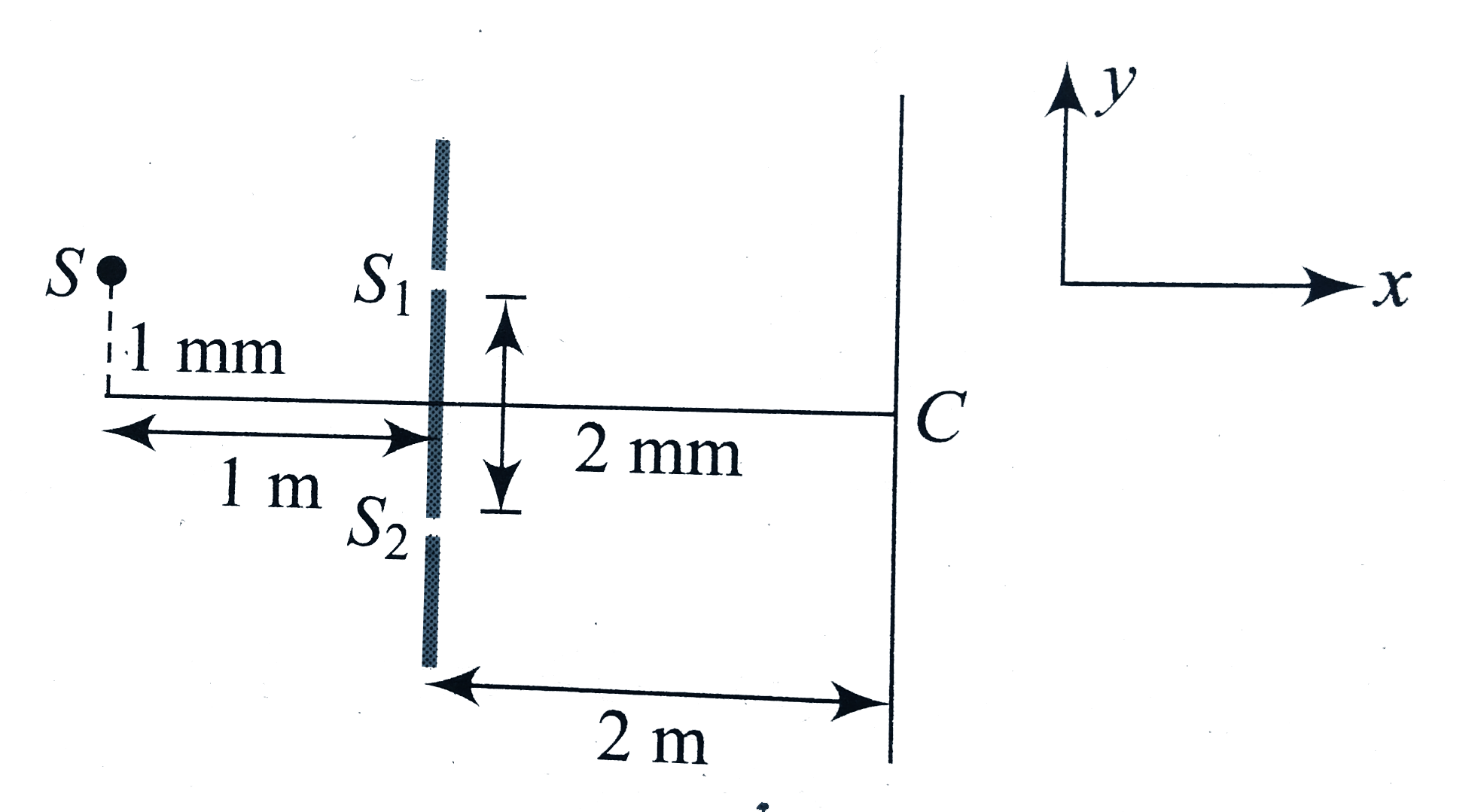
At t=0, fringe width is β1, and at t=2 s, width of figure is β2. Then
View SolutionA progressive wave is represented by the equation y=0.5sin(314t−12.56x) where y and x are in metre and t is in second .Its wavelength is
View SolutionA particles executes SHM according to the equation y = 2 sin 2πt, where y is displacement in m and t is time in s. The distance covered by the particle in 4 s of its motion is
View SolutionA particle executes S.H.M. given by the equation y = 0.45 sin 2t where y is in meter and t is in second. What is the speed of the particle when its displacement is 7.5 cm?
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
At t=2 s, the position of central maxima is
View Solution

