P=4x−z+3y
Q=−x+4z+3y
Using the definitions above for P and Q. What is 2P−Q?
7x−6z+3y
9x+2z+9y
9x−6z+3y
7x−6z+9y
The correct Answer is:C
To solve the problem, we need to find the expression for 2P−Q given the definitions of P and Q.
1. Identify the expressions for P and Q:
P=4x−z+3y
Q=−x+4z+3y
2. Calculate 2P:
2P=2(4x−z+3y)
Distributing the 2:
2P=2⋅4x+2⋅(−z)+2⋅3y=8x−2z+6y
3. Substitute Q into the expression 2P−Q:
2P−Q=(8x−2z+6y)−(−x+4z+3y)
4. Distribute the negative sign across Q:
2P−Q=8x−2z+6y+x−4z−3y
5. Combine like terms:
- Combine the x terms: 8x+x=9x
- Combine the z terms: −2z−4z=−6z
- Combine the y terms: 6y−3y=3y
Therefore, we have:
2P−Q=9x−6z+3y
6. Final Result:
The expression for 2P−Q is:
9x−6z+3y
P=4x−z+3y
Q=−x+4z+3y
2P=2(4x−z+3y)
Distributing the 2:
2P=2⋅4x+2⋅(−z)+2⋅3y=8x−2z+6y
2P−Q=(8x−2z+6y)−(−x+4z+3y)
2P−Q=8x−2z+6y+x−4z−3y
- Combine the x terms: 8x+x=9x
- Combine the z terms: −2z−4z=−6z
- Combine the y terms: 6y−3y=3y
2P−Q=9x−6z+3y
The expression for 2P−Q is:
9x−6z+3y
Topper's Solved these Questions
Similar Questions
The curve x=4−3y−y2 cuts the y-axis into two points P and Q. then the area enclosed by the y-axis and the portion of the curve which lies between P and Q is
View SolutionThe points P (4, 1) and Q (-2, 4) are reflected in line y = 3. Find the co-ordinates of P', the image of P and Q', the image of Q.
View Solution
Knowledge Check
2x+p=7x−3,2y+q=7y−3
In the above equations, p and q are constant. If q is 5 less than p, which of the following statements is true?Ax is 1 less than yBx and y equalCx is 1 more than y.Dx is 2 more than y.
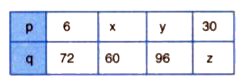
If p and q vary inversely, find the values of x,y and z.

View SolutionIf p and q vary inversely, find the values of x,y and z.

View SolutionIf the circles x2+y2+5Kx+2y+K=0 and 2x2+y2)+2Kx+3y−1=0,(K∈R) intersect at the point P and Q then the line 4x+5y−K=0 passes P and Q for :
View SolutionIf line x-2y-1=0 intersects parabola y2=4x at P and Q, then find the point of intersection of normals at P and Q.
View SolutionThe line 2x+y=3 cuts the ellipse 4x2+y2=5 at points P and Q. If θ is the angle between the normals at P and Q, then tanθ is equal to
View SolutionIF p and q are in direct variation of x, y and z in the table given below:
View SolutionP and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P' and Q in the y-axis to Q'. State the co-ordinates of P' and 'Q .
View Solution
