r=2.24+0.06t
p=2.89+0.10x
In the equation above, r and p represent the price per gallons, in dollars, of regular and premium grades of gasolin, respectively, x months after January 1 of last year. What was the cost per gallon, in dollars, of premium gasoline for the month in which the per gallons price of premium exceeded the per gallon price of regular by $0.93?
The correct Answer is:3.59
To solve the problem step by step, we will follow the given equations for the prices of regular and premium gasoline and find the month when the price of premium gasoline exceeds the price of regular gasoline by $0.93.
Step 1: Write down the equations for regular and premium gasoline prices.
- Regular gasoline price: r=2.24+0.06t
- Premium gasoline price: p=2.89+0.10x
Step 2: Set up the equation for the condition given in the problem.
We need to find when the price of premium gasoline exceeds the price of regular gasoline by $0.93. This can be expressed as:
p=r+0.93
Step 3: Substitute the expressions for p and r into the equation.
Substituting the equations we have:
2.89+0.10x=(2.24+0.06x)+0.93
Step 4: Simplify the equation.
Now, simplify the right side:
2.89+0.10x=2.24+0.06x+0.93
2.89+0.10x=3.17+0.06x
Step 5: Rearrange the equation to isolate x.
Subtract 0.06x from both sides:
2.89+0.10x−0.06x=3.17
2.89+0.04x=3.17
Now, subtract 2.89 from both sides:
0.04x=3.17−2.89
0.04x=0.28
Step 6: Solve for x.
Now, divide both sides by 0.04:
x=0.280.04
x=7
Step 7: Find the price of premium gasoline after 7 months.
Now that we have x=7, we can find the price of premium gasoline:
p=2.89+0.10(7)
p=2.89+0.70
p=3.59
Final Answer:
The cost per gallon of premium gasoline for the month in which the price exceeded the price of regular gasoline by $0.93 is $3.59.
---
- Regular gasoline price: r=2.24+0.06t
- Premium gasoline price: p=2.89+0.10x
We need to find when the price of premium gasoline exceeds the price of regular gasoline by $0.93. This can be expressed as:
p=r+0.93
Substituting the equations we have:
2.89+0.10x=(2.24+0.06x)+0.93
Now, simplify the right side:
2.89+0.10x=2.24+0.06x+0.93
2.89+0.10x=3.17+0.06x
Subtract 0.06x from both sides:
2.89+0.10x−0.06x=3.17
2.89+0.04x=3.17
0.04x=3.17−2.89
0.04x=0.28
Now, divide both sides by 0.04:
x=0.280.04
x=7
Now that we have x=7, we can find the price of premium gasoline:
p=2.89+0.10(7)
p=2.89+0.70
p=3.59
The cost per gallon of premium gasoline for the month in which the price exceeded the price of regular gasoline by $0.93 is $3.59.
Topper's Solved these Questions
Similar Questions
The set of equations above describes how the supply, S, and demand, D, for a computer memory chip depends on market price. If p represents the price in dollars on market price. If p represents the price in dollars for each lot of 10 memory chips, for whar dollars price per memory chip does supply equal demand?
View SolutionD=141−0.16p
S=64+0.28p
The set of equations above describes how the supply, S, and demand, D, for a computer memory chip depends on market price. If p represents the price in dollars for each lot of 10 memory chips, for what dollar price per memory chip does supply equal demand?
View Solution
Knowledge Check
b=2.35+0.25x
c=1.75+0.40x
In the equations above, b and c represent the price per pound, in dollars, of beef and chicken, respectively, x weeks after July 1 during last summer. What was the price per pound of beef when it was equal to the price per pound of chicken?A$2.60B$2.85C$2.95D$3.35A gas station sells regular gasoline for $2.39 per gallon and premium gasoline for $2.79 per gallon. If the gas station sold a total of 550 gallons of both types of gasoline in one day for a total of $1.344.50. how many gallons of premium gasoline were sold?
A25B75C175D475The scatterplot below compares the average gasoline prices I Boston, per gallon, to the average gasoline prices across the United States, per gallon, during a one-year period from 2017 to 2018.
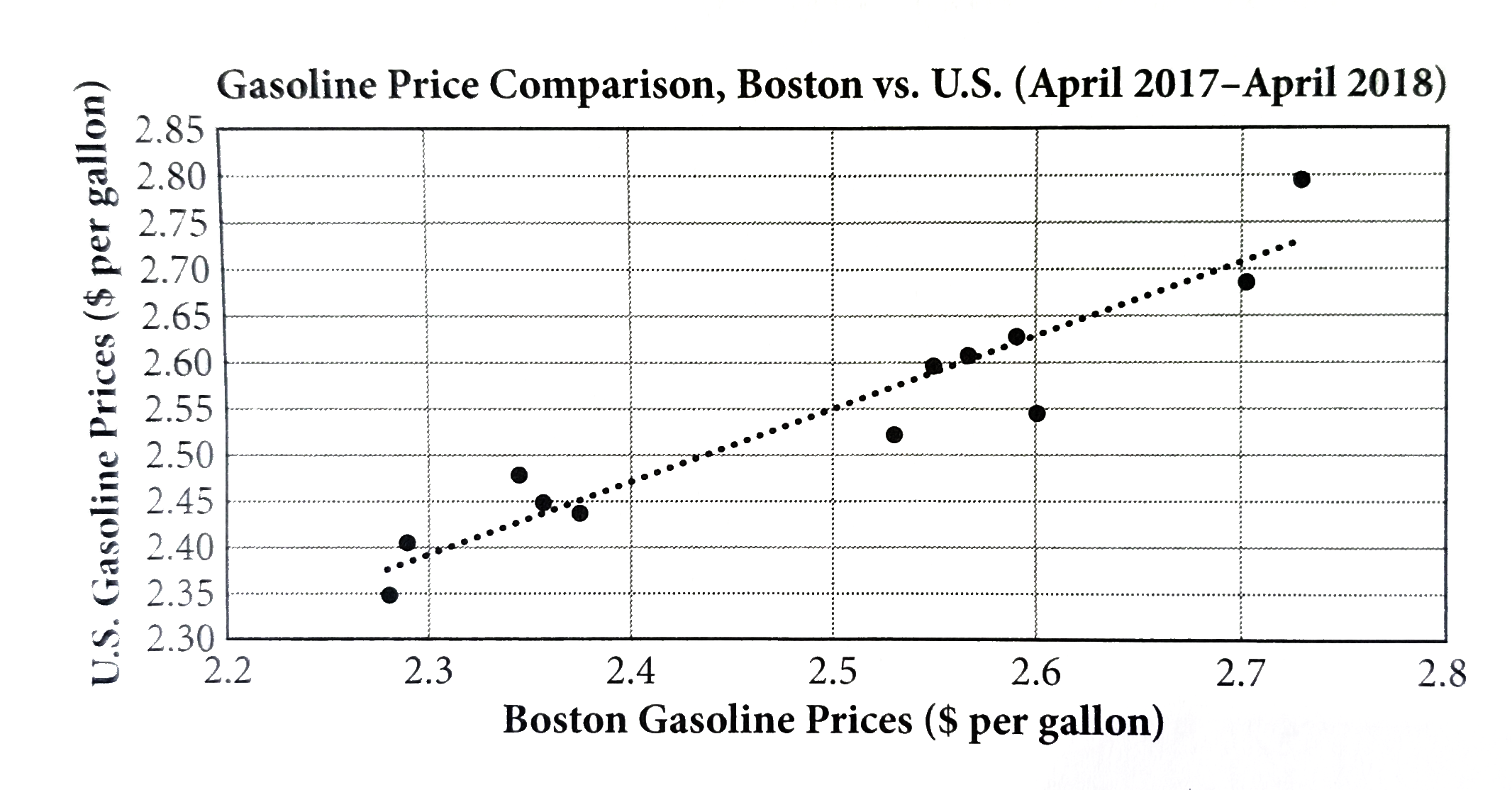
Of the following equations, whihc best modeles the data in the scatterplot ?Ay=−1.7848x+0.5842By=1.7848x+1.5842Cy=0.7848x+0.5842Dy=−0.7848x+0.5842
The demand x per month for a certain product at a price Rs p per unit is given by x=1350−45p. The cost of labour and material to manufacture is Rs 5 per unit and the fixed cost is Rs 2000 per month. What price per unit should be charged from the consumer to obtain a maximum monthly profit?
View SolutionThe demand function is x=24−2p3, where x is the number of units demanded and p is the price per unit. Find the revenue function R in terms of p.
View SolutionThe demand function is x=24−2p3 where x is the number of units demanded and p is the price per unit. Find :
(i) The revenue function R in terms of p.
(ii) The price and the number of units demanded for which the revenue is maximum.
View SolutionA study of gasoline prices across a particular state showed that the state's mean gas price was $2.87 per gallon, and the median gas price was $3.25 per gallon. Which of the following most likely accounts for the difference between the mean and median gas prices in this state?
View SolutionA bank offered a scheme of investing Rs.x per month for 2 years. If the rate of interest offered by the bank is 10% p.a, and the total interest received will be * Rs. 1,900, then the value of x is:
View Solution
