The length of a rectangle is three feet less than twice its width. If x represents the width of the rectangle, in feet, which inequality represents the area of the rectangle that is at most 30 square feet?
x(3-2x)ge30'
The correct Answer is:A
To solve the problem step by step, we need to define the variables and set up the inequality based on the information given.
Step 1: Define the Variables
Let x represent the width of the rectangle in feet.
Step 2: Express the Length in Terms of Width
According to the problem, the length of the rectangle is three feet less than twice its width. Therefore, we can express the length L as:
L=2x−3
Step 3: Write the Expression for the Area
The area A of a rectangle is given by the formula:
A=length×width
Substituting the expressions we have:
A=x⋅(2x−3)
Step 4: Set Up the Inequality for the Area
We are told that the area of the rectangle is at most 30 square feet. This can be expressed as:
x(2x−3)≤30
Step 5: Rearrange the Inequality
To make it clearer, we can rearrange the inequality:
2x2−3x≤30
Subtract 30 from both sides:
2x2−3x−30≤0
Step 6: Identify the Correct Inequality
The inequality that represents the area of the rectangle that is at most 30 square feet is:
2x2−3x−30≤0
Final Answer
Thus, the correct inequality representing the area of the rectangle that is at most 30 square feet is:
x(2x−3)≤30
Let x represent the width of the rectangle in feet.
According to the problem, the length of the rectangle is three feet less than twice its width. Therefore, we can express the length L as:
L=2x−3
The area A of a rectangle is given by the formula:
A=length×width
Substituting the expressions we have:
A=x⋅(2x−3)
We are told that the area of the rectangle is at most 30 square feet. This can be expressed as:
x(2x−3)≤30
To make it clearer, we can rearrange the inequality:
2x2−3x≤30
Subtract 30 from both sides:
2x2−3x−30≤0
The inequality that represents the area of the rectangle that is at most 30 square feet is:
2x2−3x−30≤0
Thus, the correct inequality representing the area of the rectangle that is at most 30 square feet is:
x(2x−3)≤30
Topper's Solved these Questions
Similar Questions
Knowledge Check
The length of a rectangle is 2 ft shorter than twice the width . Which of the following graphs represents the area of the rectangle in terms of its width ?
A B
B C
C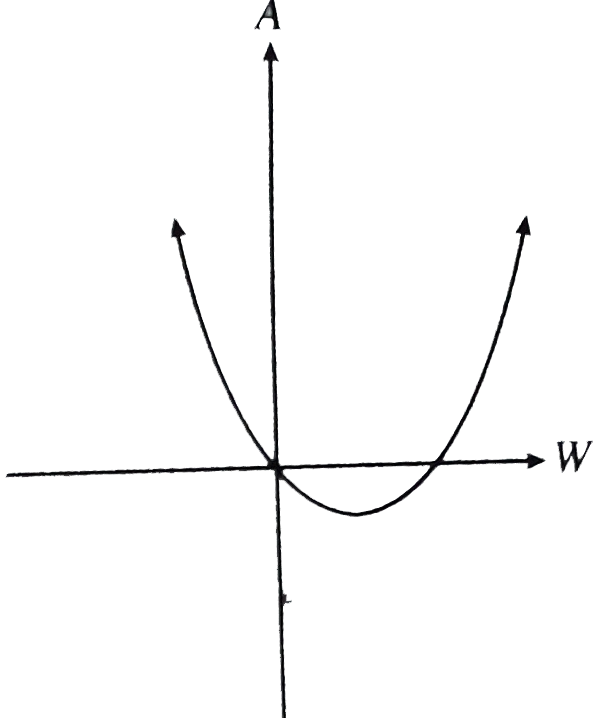 D
D
The length of a certain rectangle is twice the width. If the area of the rectangle is 128, what is the length of the rectangle.
A4B8C16D2113The area of a rectangle is 300 square meters, and its length is 3 times its width. How many meters wide is the rectangle?
A10B30C50D100
The length of a rectangle is 4 units less than thrice its breadth. If the breadth is y units, find the rule for finding the perimeter of the rectangle.
View SolutionThe length of a rectangle is 7.1 cm and its breadth is 2.5 cm. Whatis the area of the rectangle?
View SolutionThe length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If area of the rectangle is three times the area of the square, find the dimensions of each.
View SolutionThe perimeter of a rectangular field is 35 km. If the length of the field is twice its width, find the area of the rectangle in sq. metres.
View SolutionIf the length of a rectangle is increased by 40%, and the width of the same rectangle is decreased by 40%, then the area of the rectangle is decreased by x% . What is the value of x ?
View Solution
