Question

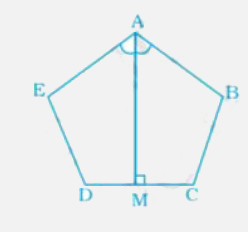
$ABCDE$
is a regular pentagon. The bisector of $\angle A$
of the pentagon meets the side $CD$
in $M$
Show that $\angle AMC={90}^{\circ }$ In pentagon $ABCDE$

Explanation

In`A B C D E` pentagon
interior angle `=(5-2)xx180^0/5`
`=108^0`
in `ABCM` by angle sum
`/_B+/_C+/_BAM+/_AMC=360^0`
`108^0+108^0+54^0+/_AMC=360^0`
`/_AMC=90^0`