Question

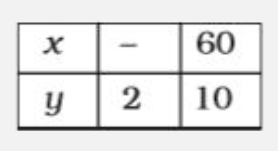
If $xandy$
vary inversely as each other, and $x=10$
when $y=6.$
Find $y$
when $x=15$

Explanation

To solve the problem step by step, we will use the concept of inverse variation.

1. Understand the relationship: Since \( x \) and \( y \) vary inversely, we can express this relationship as:
\( x \cdot y = k \)
where \( k \) is a constant.

2. Find the constant \( k \): We are given that \( x = 10 \) when \( y = 6 \). We can substitute these values into the equation to find \( k \):
\( k = 10 \cdot 6 = 60 \)

3. Set up the equation for the new values: Now we need to find \( y \) when \( x = 15 \). Using the relationship we established, we can set up the equation:
\( 15 \cdot y = 60 \)

4. Solve for \( y \): To find \( y \), we can rearrange the equation:
\( y = \frac{60}{15} \)
Simplifying this gives:
\( y = 4 \)

5. Conclusion: Therefore, when \( x = 15 \), the value of \( y \) is \( 4 \).

Final Answer:
When \( x = 15 \), \( y = 4 \).