A class has 12 boys and 4 girls. If three students are selected at random from the class,
what is the probability that all will be boys?
155
14
13
1128
The correct Answer is:D
To find the probability that all three selected students are boys from a class of 12 boys and 4 girls, we can follow these steps:
Step 1: Determine the total number of students
The total number of students in the class is:
12 (boys)+4 (girls)=16 (total students)
Step 2: Calculate the probability of selecting a boy on the first selection
The probability of selecting a boy first is:
P(1st boy)=Number of boysTotal number of students=1216
Step 3: Update the number of boys and total students after the first selection
After selecting one boy, the remaining students are:
- Boys: 12−1=11
- Girls: 4
- Total remaining students: 16−1=15
Step 4: Calculate the probability of selecting a boy on the second selection
The probability of selecting a boy second is:
P(2nd boy)=1115
Step 5: Update the number of boys and total students after the second selection
After selecting another boy, the remaining students are:
- Boys: 11−1=10
- Girls: 4
- Total remaining students: 15−1=14
Step 6: Calculate the probability of selecting a boy on the third selection
The probability of selecting a boy third is:
P(3rd boy)=1014
Step 7: Calculate the combined probability of all three selections being boys
The combined probability of all three selections being boys is the product of the individual probabilities:
P(all boys)=P(1st boy)×P(2nd boy)×P(3rd boy)
=1216×1115×1014
Step 8: Simplify the expression
Now, we can simplify the expression:
=12×11×1016×15×14
We can simplify this step-by-step:
- 1216=34
- 1014=57
So now we have:
=34×1115×57
Now multiplying:
=3×11×54×15×7
=165420
Step 9: Further simplify
Now, we can simplify 165420:
Both numbers can be divided by 15:
=1128
Final Answer
Thus, the probability that all three selected students are boys is:
1128
The total number of students in the class is:
12 (boys)+4 (girls)=16 (total students)
The probability of selecting a boy first is:
P(1st boy)=Number of boysTotal number of students=1216
After selecting one boy, the remaining students are:
- Boys: 12−1=11
- Girls: 4
- Total remaining students: 16−1=15
The probability of selecting a boy second is:
P(2nd boy)=1115
After selecting another boy, the remaining students are:
- Boys: 11−1=10
- Girls: 4
- Total remaining students: 15−1=14
The probability of selecting a boy third is:
P(3rd boy)=1014
The combined probability of all three selections being boys is the product of the individual probabilities:
P(all boys)=P(1st boy)×P(2nd boy)×P(3rd boy)
=1216×1115×1014
Now, we can simplify the expression:
=12×11×1016×15×14
We can simplify this step-by-step:
- 1216=34
- 1014=57
=34×1115×57
=3×11×54×15×7
=165420
Now, we can simplify 165420:
Both numbers can be divided by 15:
=1128
Thus, the probability that all three selected students are boys is:
1128
Topper's Solved these Questions
- PROBABILITY Book:ENGLISH SATChapter:PROBABILITY Exercise:EXERCISES
Explore 16 Videos
- PRACTICE TEST 5 - MATHEMATICS TESTBook:ENGLISH SATChapter:PRACTICE TEST 5 - MATHEMATICS TESTExercise:EXERCISE
Explore 60 Videos
- PROBLEM SOLVING AND DATA ANALYSISBook:ENGLISH SATChapter:PROBLEM SOLVING AND DATA ANALYSISExercise:EXERICSE
Explore 80 Videos
Similar Questions
A class consists of 10 boys and 8 girls. Three students are selected at random. What is the probability that the selected group has (i) all boys? (ii) all girls? (iii) at least one girl?
View SolutionIn a group of students , there are 3 boys and 3 girls . Four students are to be selected at random from the group . Find the probability that either 3 boys and 1 girl or 3 girls and 1 boy are selected .
View SolutionIn a medical examination of students of a class, the following blood groups are recorded.
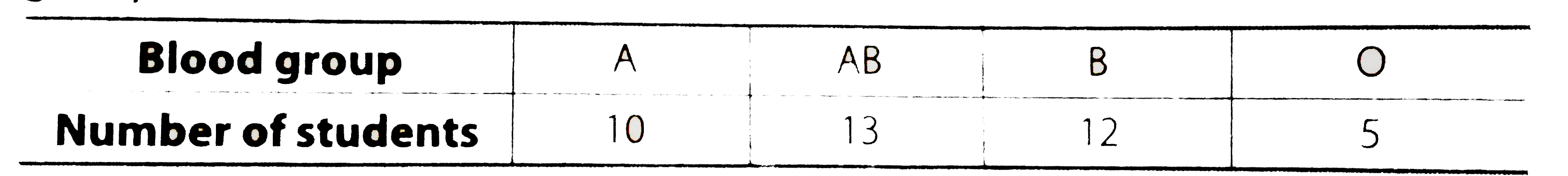
A student is selected at random from the class. The probability that he/she has blood group B, is
View SolutionA class consists of 50 students out of which there are 10 girls. In the class 2 girls and 5 boys are rank holders in an examination. If a student is selected at random from the class and is found to be a rank holder, what is the probability that the student selected is a girl?
View SolutionIn a class, 5% of the boys and 10% of the girls have an IQ of more than 150. In this class 60% of the students are boys. If a student is selected at random and found to have an IQ of more than 150, find the probability that the student is a boy.
View SolutionA class has 20 girls and 16 boys. One student is selected at random. Find the probability that the student is a girl.
View SolutionOut of 9 outstanding students in a college, there are 4 boys and 5 girls. A team of four students is to be selected for a quiz programme. Find the probability that two are boys and two are girls.
View SolutionIn a class of 50 students, 20 are boys and rest are girls. A student is selected at random. Find the probability of selecting a boy.
View SolutionIn a certain college, 4% of boys and 1% of girls are taller than 1.75 metres. Furthermore, 60% of the students in the college are girls. A student is selected at random from the college and is found to be taller than 1.75 metres. Find the probability that the selected student is a girl.
View SolutionIn a certain college, 4% of boys and 1% of girls are taller than 1.75 metres. Furthermore, 60% of the students in the college are girls. A student is selected at random from the college and is found to be taller than 1.75 metres. Find the probability that the selected student is a girl.
View Solution

