Let vector →V=(2,3) and vector →U=(6,−4).
(ii) What is norm of →U ?
To find the norm (or magnitude) of the vector →U=(6,−4), we can follow these steps:
1. Identify the components of the vector:
The vector →U has components x=6 and y=−4.
2. Use the formula for the magnitude of a vector:
The magnitude (or norm) of a vector →U=(x,y) is given by the formula:
∥→U∥=√x2+y2
3. Substitute the components into the formula:
Substitute x=6 and y=−4 into the formula:
∥→U∥=√62+(−4)2
4. Calculate the squares of the components:
Calculate 62 and (−4)2:
62=36and(−4)2=16
5. Add the squares:
Now, add the results:
36+16=52
6. Take the square root:
Finally, take the square root of the sum:
∥→U∥=√52
7. Simplify the square root if necessary:
The square root of 52 can be simplified:
√52=√4×13=2√13
Final Answer:
The norm of →U is √52 or 2√13.
---
The vector →U has components x=6 and y=−4.
The magnitude (or norm) of a vector →U=(x,y) is given by the formula:
∥→U∥=√x2+y2
Substitute x=6 and y=−4 into the formula:
∥→U∥=√62+(−4)2
Calculate 62 and (−4)2:
62=36and(−4)2=16
Now, add the results:
36+16=52
Finally, take the square root of the sum:
∥→U∥=√52
The square root of 52 can be simplified:
√52=√4×13=2√13
The norm of →U is √52 or 2√13.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
Let vector →V=(2,3) and vector →U=(6,−4).
Are →Uand→V perpendicular?
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
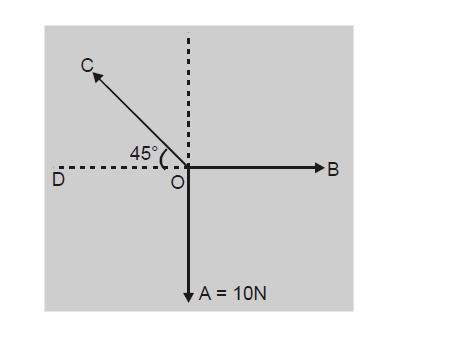
(ii) What is the magnitude of vector −−→OC ?
View SolutionThe angle between two vectors →uand→v is 60∘ .Find (i) the scalar product of the two vectors and (ii) the vector product of the two vectors , if →u=7units,→v=14 units ?
View SolutionA vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
View SolutionAt what angle two vectors →P=2Nand→Q=3N act such that their sum is 4 N .
View SolutionLet →A=ˆiAcosθ+ˆjAsinθ, be any vector. Another vector →B which is normal to →A is :-
View SolutionLet →A=ˆiAcosθ+ˆjsinθ, be any vector. Another vector →B which is normal to →A is :
View Solution

