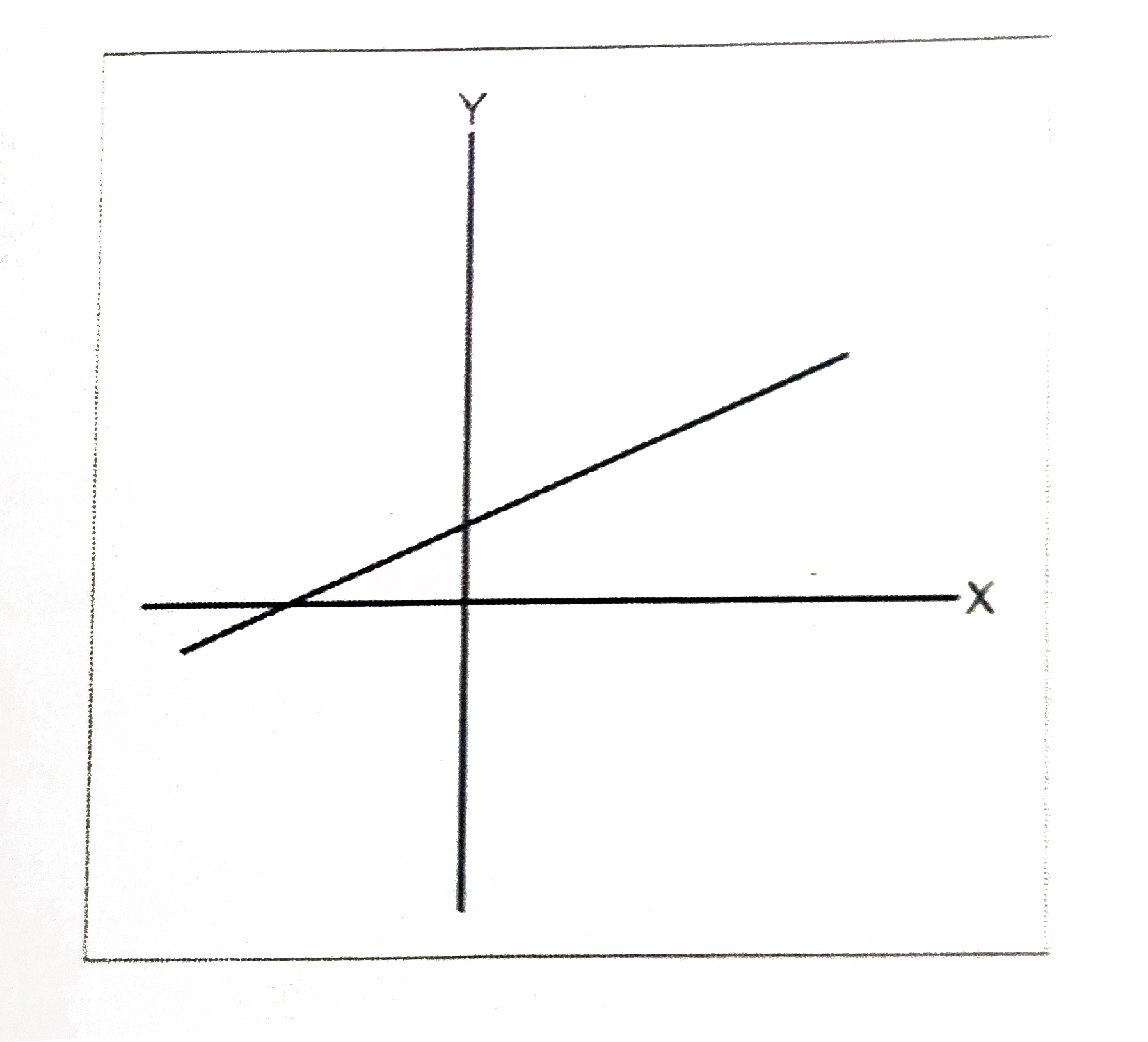If the segment of the line y=−2x+2 that lies in quadrant I is rotated about the y-axis , a cone is formed . What is the volume of the cone ?
To find the volume of the cone formed by rotating the segment of the line y=−2x+2 that lies in the first quadrant about the y-axis, we can follow these steps:
Step 1: Find the points where the line intersects the axes
To determine the segment of the line in the first quadrant, we need to find the x-intercept and y-intercept of the line.
1. Y-intercept: Set x=0:
y=−2(0)+2=2
So, the y-intercept is (0,2).
2. X-intercept: Set y=0:
0=−2x+2⟹2x=2⟹x=1
So, the x-intercept is (1,0).
Step 2: Identify the dimensions of the cone
The segment of the line in the first quadrant is between the points (0,2) and (1,0). When this segment is rotated about the y-axis, it forms a cone.
- Height (h) of the cone: The height is the y-coordinate of the y-intercept, which is 2.
- Radius (r) of the cone: The radius is the x-coordinate of the x-intercept, which is 1.
Step 3: Use the formula for the volume of a cone
The volume V of a cone is given by the formula:
V=13πr2h
Substituting the values of r and h:
V=13π(1)2(2)
V=13π⋅1⋅2=2π3
Final Answer
Thus, the volume of the cone formed is:
2π3
---
To determine the segment of the line in the first quadrant, we need to find the x-intercept and y-intercept of the line.
y=−2(0)+2=2
So, the y-intercept is (0,2).
0=−2x+2⟹2x=2⟹x=1
So, the x-intercept is (1,0).
The segment of the line in the first quadrant is between the points (0,2) and (1,0). When this segment is rotated about the y-axis, it forms a cone.
- Radius (r) of the cone: The radius is the x-coordinate of the x-intercept, which is 1.
The volume V of a cone is given by the formula:
V=13πr2h
Substituting the values of r and h:
V=13π(1)2(2)
V=13π⋅1⋅2=2π3
Thus, the volume of the cone formed is:
2π3
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY Book:ENGLISH SATChapter:THREE DIMENSIONAL GEOMETRY Exercise:EXERCISE
Explore 6 Videos
- STRATEGIES FOR SOLVING SAT MATH PROBLEMS Book:ENGLISH SATChapter:STRATEGIES FOR SOLVING SAT MATH PROBLEMS Exercise:EXAMPLE
Explore 19 Videos
- TRANSFORMATION AND SYMMETRYBook:ENGLISH SATChapter:TRANSFORMATION AND SYMMETRYExercise:EXERCISES
Explore 4 Videos
Similar Questions
Knowledge Check
If the region bounded by the lines y=−43x+4 , x=0 , and y=0 is rotated about the y-axis, the volume of the figure formed is
A18.8B37.7C56.5D84.8The region in the first quadrant bounded by the line 3x+2y=7 and the coordinate axes is rotated about the x-axis .What is the volume of the resulting solid ?
A8 units3B20 units3C30 units3D40 units3
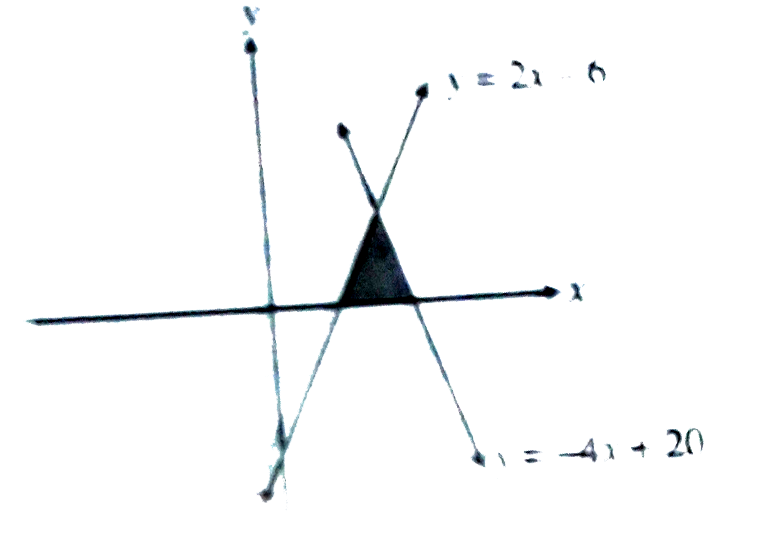
Find the area of the triangle that lies in the first quadrant , with its base on the x-axis and that is bounded by the lines y=2x-6 and y=-4x+20 (the shaded area in the diagram shown above).
View SolutionThe sum of the legs of a right triangle is 9 cm. When the triangle rotates about one of the legs, a cone result which has the maximum volume. Then
View SolutionThe area of the base of a right circular cone is 314cm2 and its height is 15cm. Find the volume of the cone.
View SolutionThe area of the base of a right circular cone is 314cm2 and its height is 15cm. Find the volume of the cone.
View SolutionThe base radius and slant height of a cone are 8 cm and 2√13cm respectively. Find the volume of the cone.
View SolutionPoint A lies on the line y=2x and the sum of its abscissa and ordinate is 12. Point B lies on the x-axis and the line AB is perpendicular to the line y=2x. Let O be the origin. The area of the Delta AOB is
View Solution