Graph the parametric euation {x=3t+4y=t−5
To graph the parametric equations given by x=3t+4 and y=t−5, we will follow these steps:
Step 1: Eliminate the parameter t
We start by expressing t in terms of y from the equation for y:
y=t−5⟹t=y+5
Step 2: Substitute t into the equation for x
Next, we substitute t into the equation for x:
x=3t+4=3(y+5)+4
Now, simplify this equation:
x=3y+15+4=3y+19
Step 3: Rearrange to find the relationship between x and y
Rearranging the equation gives:
3y=x−19⟹y=x−193
Step 4: Identify the slope and intercept
This equation y=13x−193 is in the slope-intercept form y=mx+c, where:
- The slope m=13 indicates that the line rises as it moves to the right.
- The y-intercept c=−193.
Step 5: Find points for graphing
To graph this line, we can find a couple of points:
1. When x=0:
y=0−193=−193≈−6.33
So, one point is (0,−193).
2. When y=0:
0=x−193⟹x−19=0⟹x=19
So, another point is (19,0).
Step 6: Plot the points and draw the line
Now, we can plot the points (0,−193) and (19,0) on the Cartesian plane. Draw a straight line through these points to represent the graph of the parametric equations.
Summary of the Graph
The graph of the parametric equations x=3t+4 and y=t−5 is a straight line with:
- x-intercept at (19,0)
- y-intercept at (0,−193)
We start by expressing t in terms of y from the equation for y:
y=t−5⟹t=y+5
Next, we substitute t into the equation for x:
x=3t+4=3(y+5)+4
Now, simplify this equation:
x=3y+15+4=3y+19
Rearranging the equation gives:
3y=x−19⟹y=x−193
This equation y=13x−193 is in the slope-intercept form y=mx+c, where:
- The slope m=13 indicates that the line rises as it moves to the right.
- The y-intercept c=−193.
To graph this line, we can find a couple of points:
1. When x=0:
y=0−193=−193≈−6.33
So, one point is (0,−193).
0=x−193⟹x−19=0⟹x=19
So, another point is (19,0).
Now, we can plot the points (0,−193) and (19,0) on the Cartesian plane. Draw a straight line through these points to represent the graph of the parametric equations.
The graph of the parametric equations x=3t+4 and y=t−5 is a straight line with:
- x-intercept at (19,0)
- y-intercept at (0,−193)
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the graph of the parametric equation {x=t2+ty=t2−t
Ax≥0Bx≥−14Cx is any real numberDx≥−1If 0≤t≤1, which of the following graphs is the graph of y versus x where x and y are related by the parametric equations y=t2 and x=√t ?
A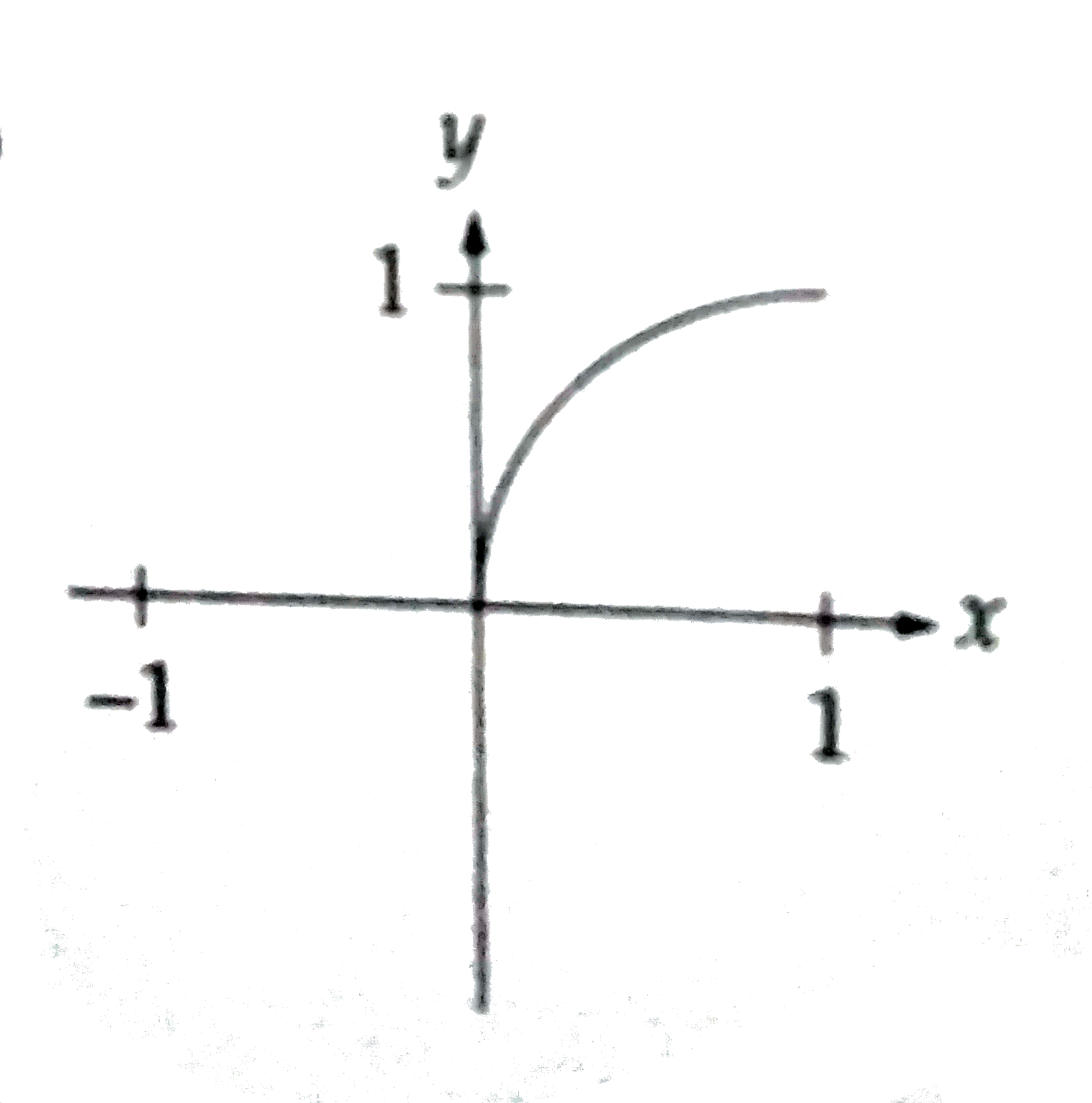 B
B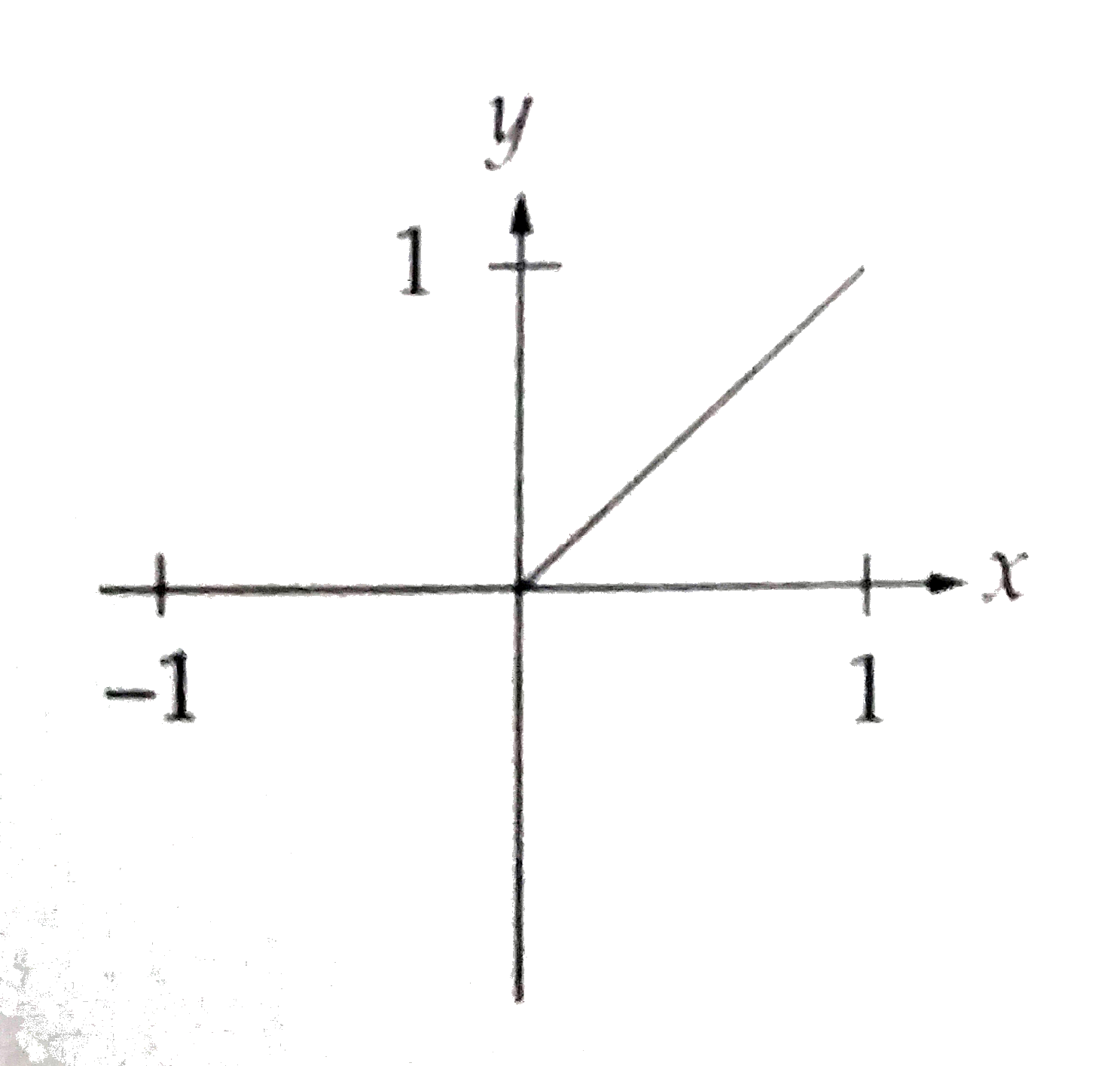 C
C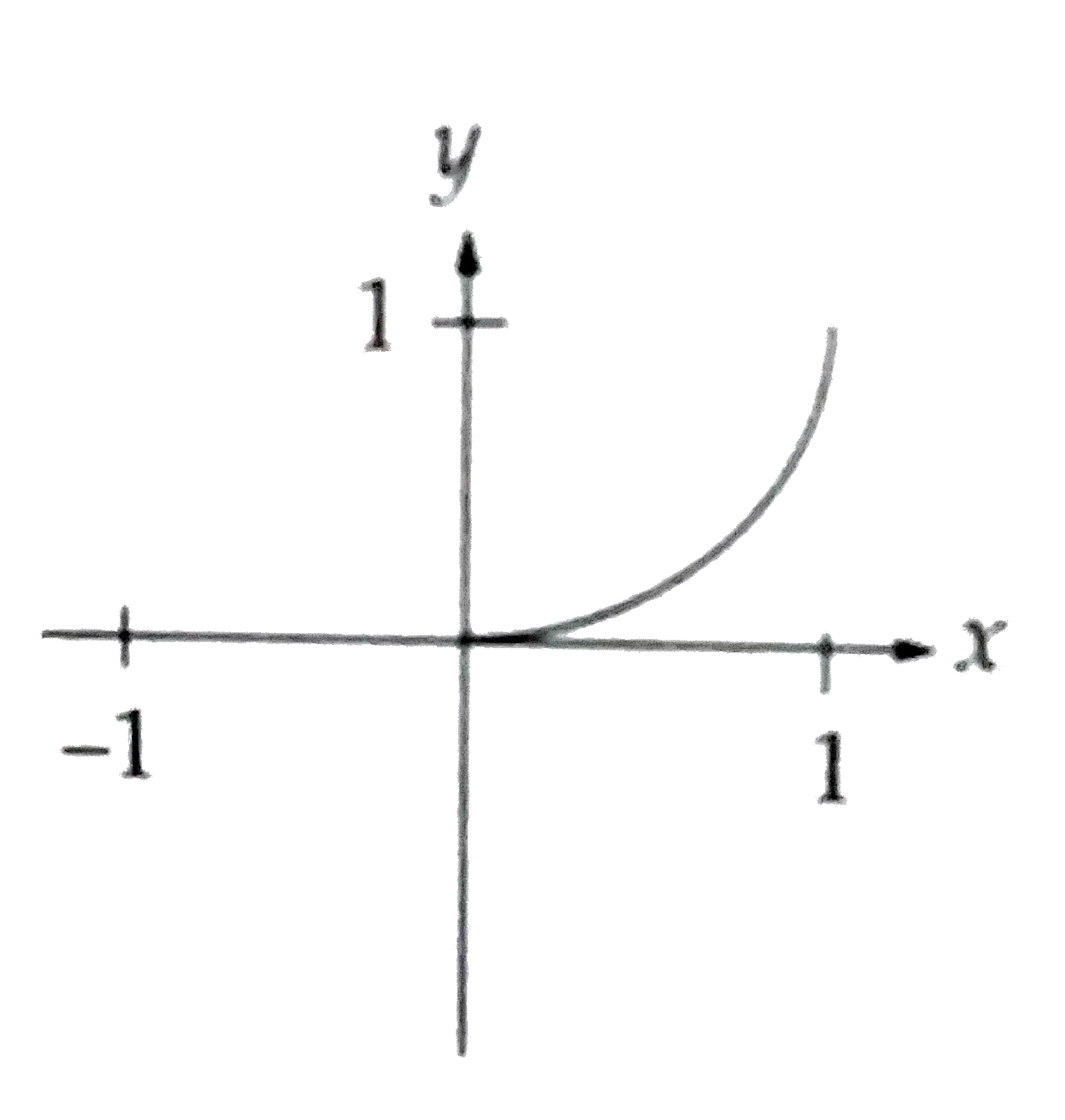 D
D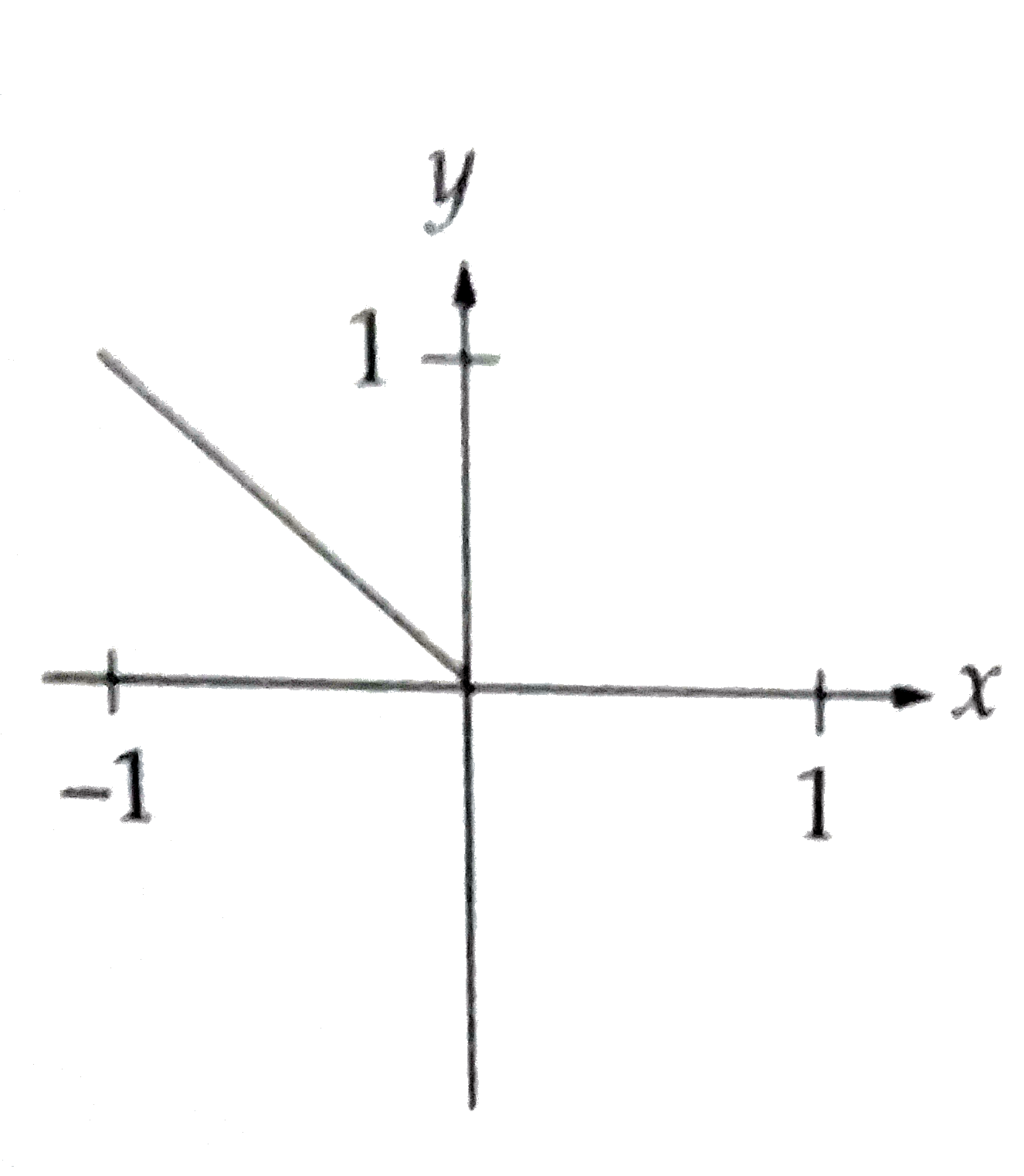
The graph of y=(x+2)(2x-3) can be expressed as a set of parametric equations. If x=2t-2 and y=f(t) , then f(t)=
A2t(4t-5)B(2t-2)(4t-7)C2t(4t-7)D(2t-2)(4t-5)
Find the cartesian equation of the curve whose parametric equations are :
x=t,y=t2
View SolutionShow that the function y=f(x) defined by the parametric equations x=etsin(t),y=et.cos(t), satisfies the relation y''(x+y)2=2(xy'−y)
View SolutionThe length of latusrectum of the parabola whose parametric equations are x=t2+t+1,y=t2−t+1, where t∈R is equal to (1) √2 (2) √4 (3) √8 (4) √6
View SolutionFind the Cartesian equation of the curves whose parametric equation are : x=20t4+t2,y=5(4−t2)4+t2
View SolutionIf a curve is represented parametrically by the equation x=f(t)andy=g(t) then prove that d2ydx2=−[g'(t)f'(t)]3(d2xdy2)
View Solution

