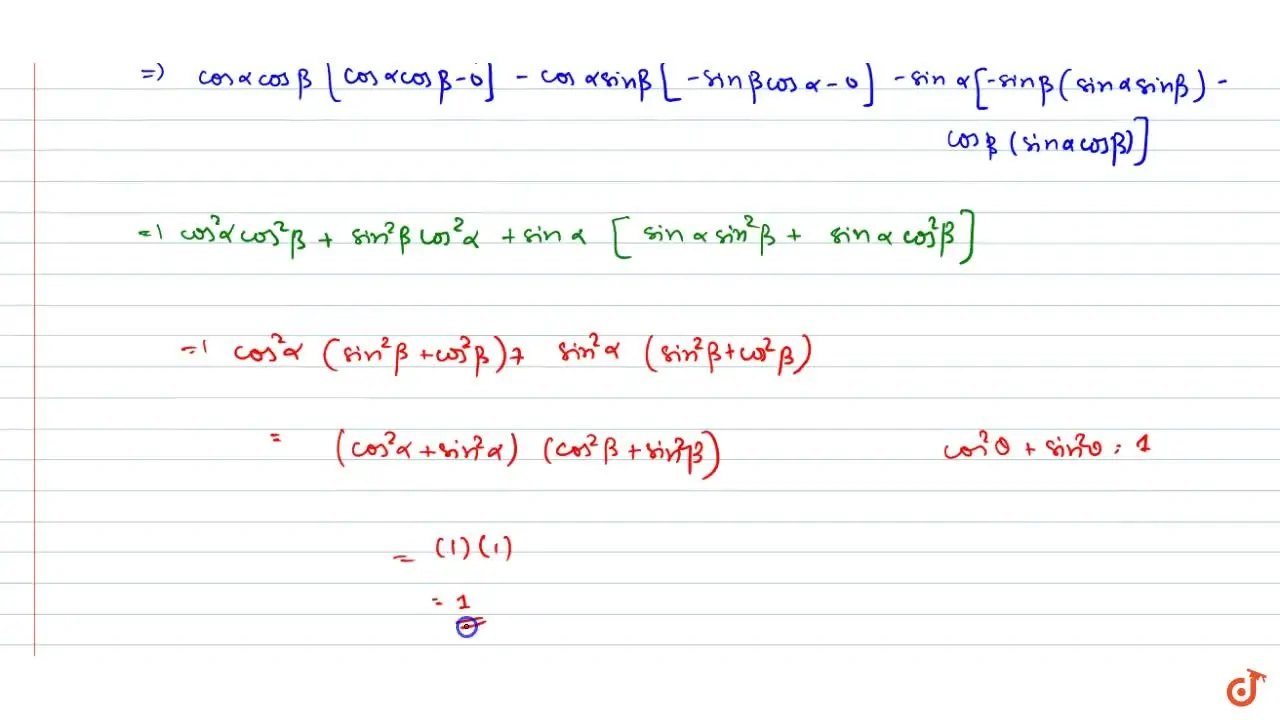Evaluate
Given
If we follow row wise operation we get
Expanding with respect to first row
Related Playlists
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.45videos
DETERMINANTS
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - SOLVED EXAMPLES34videos
DETERMINANTS
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - QUESTION3videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
Similar Questions
Evaluate
∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣View Solution∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣ is equal to
View SolutionProve that ∣∣ ∣ ∣∣cosαcosβcosαsinβsinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣=cos2α
View SolutionIf cosα+cosβ=0=sinα+sinβ, then cos2α+cos2β=?
View Solution(1+cosαcosβ)2−(cosα+cosβ)2=
View SolutionEvaluate :
Δ=∣∣ ∣ ∣∣0sinα−cosα−sinα0sinβcosα−sinβ0∣∣ ∣ ∣∣.View SolutionThe determinant D=∣∣ ∣ ∣∣cos(α+β)−sin(α+β)cos2βsinαcosαsinβ−cosαsinαcosβ∣∣ ∣ ∣∣ is independent of :-
View SolutionIf A=⎡⎢⎣0sinαsinαsinβ−sinα0cosαcosβ−sinαsinβ−cosαcosβ0⎤⎥⎦ then (A) |A| is independent of αandβ (B) A−1 depends only on beta (C) A−1 does not exist (D) none of these
View SolutionShow by vector method that sin(α−β)=sinαcosβ−cosαsinβ.
View SolutionShow without expanding at any stage that: ∣∣ ∣ ∣∣1cosα−sinαcosα+sinα1cosβ−sinβcosβ+sinβ1cosγ−sinγcosγ+sinγ∣∣ ∣ ∣∣=2 ∣∣ ∣ ∣∣1cosαsinα1cosβsinβ1cosγsinγ∣∣ ∣ ∣∣
View Solution