volume and capacity.
Volume and Capacity
Understanding capacity, volume, capacity factor, volume formula, etc is very important. In this chapter, we will try to understand these terms. In the end, we would solve some examples to better understand the concept of volume and capacity.
What is Capacity?
When the hollow objects are filled with liquid or air, then it takes the shape of the container.
The amount of matter that an object can contain within itself is known as the capacity. Even after many similarities of volume and capacity, we can still distinguish between them. Capacity can be measured in m3, cm3, pounds, millilitres, and gallons, etc.
What is Volume?
Any object that has got length, breadth, and thickness happens to be a 3-dimensional figure. The volume is the measurement of the total space in 3-D, which is occupied by a solid. The volume of a hollow 3-dimensional figure is the difference between the space occupied by the body and the total amount of space that is left inside the hollow body. In our daily life, we come across a lot of different hollow objects.
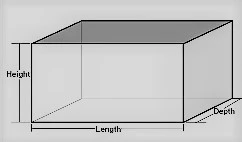
When it comes to the units for measuring volume, they are m3, cm3, litre, millilitre, etc. If we use cuboid as an example, it is bounded by six rectangular faces and is a solid figure. So, in the case of cuboids, the dimensions are length (l), breadth (b), and height (h.)
Therefore, the volume of a cuboid is V = l x b x h
Difference between Volume and Capacity
As mentioned that although both capacity and volume have similar qualities, still we can find some differences between them
Let us summarise, as shown in the table below:
Volume
Capacity
The amount of three-dimensional space that a 3D-object occupies
Ability of something (like a solid substance, gas, liquid) to hold, absorb or receive
Common units- cm3, m3
Common-units - litre, gallons, pounds
Example - cube, cuboid
Example- cone, cylinder
We will try to explain the differences between volume and capacity with an example.
A teacup has the capacity of 100 ml, but the volume of the cup is 150 ml. It shows that the cup has the capacity to accommodate 100 ml whereas the cup occupies around 150 ml of space. The reason behind this is that 100 ml is the hollow space that can be occupied by tea or any other material whereas the remaining 50 ml of space is occupied by the material from which the tea mug is made. So, you have understood the differences between the capacity and the volume. Moving on, we will now study volume formula, which is another very important topic.
Related Videos:
- Various units of measurement of area
- Units of measurement of length
- Area and perimeters of various plane
- Area of trapezium ABCD
What is Volume formula?
The amount of space that an object or substance takes up is known as the volume. It is measured in terms of cubic units. It is the capacity of the container to hold the amount of gas or liquid. With the use of arithmetic formula, the volume of 3-dimensional mathematical shapes can be easily calculated such as cylinder, cuboid, cube, cone, prism, etc. One can try to make use of integral calculus to find the volumes of complicated shapes.

We can take an example that the volume of a cylinder is measured by
πr2h, where r = d⁄2
Here d = diameter of the circular base
r = radius of the circular base
Volume Formulas of Various Geometric Figures
Let us concentrate on some of the formulas where the volumes of basic shapes can be found:
Shapes
Volume Formula
Variables
Rectangular Solid or Cuboid
V = l × w × h
l = Length,
w = Width,
h = Height
Cube
V = a3
a = length of edge or side
Cylinder
V = πr2h
r = radius of the circular edge,
h = height
Prism
V = B × h
B = area of base, (B = side2 or length.breadth)
h = height
Sphere
V = (4⁄3) πr3
r = radius of the sphere
Pyramid
V = (1⁄3) × B × h
B = area of the base,
h = height of the pyramid
Right Circular Cone
V = (1⁄3)πr2h
r = radius of the circular base,
h = height (base to tip)
Square or Rectangular Pyramid
V = (1⁄3) × l × w × h
l = length of the base,
w = width of base,
h = height (base to tip)
Ellipsoid
V = (4⁄3) × π × a × b × c
a, b, c = semi-axes of ellipsoid
Tetrahedron
V = a3⁄ (6 √2)
a = length of the edge
Now, we will concentrate on the problems and solutions below:
Question: There is a vessel of 3 liters and 500 ml of curd. Can you calculate as to how many glasses each of 25 ml capacity can be filled?
Answer: Capacity of curd in a vessel = 3 liters 500 ml = 3 × 1000 ml + 500 ml = 3500 ml
The capacity of one glass = 25ml
Here, the number of glasses that can be filled = 3500/25
Therefore, the number of glasses that can be filled by curd = 140
Question: Find the volume and the total surface area of a cuboid, whose:
(i) Length = 20 cm, breadth = 15 cm and height = 10 cm.
Answer: We know that
Volume of a cuboid =Length× Breadth × Height
= 20 × 15 × 10 =3000cm3
The total surface area of a cuboid
= 2(l × b + b × h + h × l)
= 2(20 x 15 + 15 × 10 + 10 × 20)
= 2(300 + 150 + 200)
= 2 × 650
=1300 cm2
(ii) l = 7.5, b = 4.6m and h = 90cm,
Answer:
Here, Length = 7.5m
breadth = 4.6m,
height = 90cm =90/100m=0.9m.
Volume of a cuboid
= l × b × h
= 7.5 × 4.6 × 0.9
= 31.05 m3
The total surface area of a cuboid
= 2(l × b + b × h + h × l)
= 2(7.5 × 4.6 + 4.6 × 0.9 + 0.9 × 7.5)
= 2(34.5 + 4.14 + 6.75)
= 2(45.39)
= 22.69 m2
So, we can say that the total surface area of a cuboid of the given figure is 22.69 m2.
Important Chapters:
- NCERT Solutions for Maths
- NCERT Solution for Class 6 Maths Chapter Mensuration
- NCERT Solution for Class 8 Maths Chapter Mensuration
- NCERT Solution for Class 9 Maths Chapter Surface Area and Volume

Volume
Capacity
The amount of three-dimensional space that a 3D-object occupies
Ability of something (like a solid substance, gas, liquid) to hold, absorb or receive
Common units- cm3, m3
Common-units - litre, gallons, pounds
Example - cube, cuboid
Example- cone, cylinder

Shapes
Volume Formula
Variables
Rectangular Solid or Cuboid
V = l × w × h
l = Length,
w = Width,
h = Height
Cube
V = a3
a = length of edge or side
Cylinder
V = πr2h
r = radius of the circular edge,
h = height
Prism
V = B × h
B = area of base, (B = side2 or length.breadth)
h = height
Sphere
V = (4⁄3) πr3
r = radius of the sphere
Pyramid
V = (1⁄3) × B × h
B = area of the base,
h = height of the pyramid
Right Circular Cone
V = (1⁄3)πr2h
r = radius of the circular base,
h = height (base to tip)
Square or Rectangular Pyramid
V = (1⁄3) × l × w × h
l = length of the base,
w = width of base,
h = height (base to tip)
Ellipsoid
V = (4⁄3) × π × a × b × c
a, b, c = semi-axes of ellipsoid
Tetrahedron
V = a3⁄ (6 √2)
a = length of the edge
Similar Questions
Knowledge Check
From the following relationship between respiration volumes and capacities, mark the correct option.
(i) Inspiratory Capacity (IC) = Tidal Volume + Residual Volume
(ii) Vital Capacity (VC) = Tidal Volume (TV) + Inspiratory Reserve Volume (IRV) + Expiratory Reserve Volume (ERV)
(iii) Residual Volume (RV) = Vital Capacity (VC) - Inspiratory Reserve Volume (IRV)
(iv) Tidal Volume (TV) = Inspiratory Capacity (IC) - Inspiratory Reserve Volume (IRV)A(i) Incorrect, (ii) Incorrect, (iii) Incorrect, (iv) CorrectB(i) Incorrect, (ii) Correct, (iii) Incorrect, (iv) CorrectC(i) Correct, (ii) Correct, (iii) Incorrect, (iv) CorrectD(i) Correct, (ii) Incorrect, (iii) Correct, (iv) IncorrectGiven figure is showing spirogram of pulmonary volumes and capacities
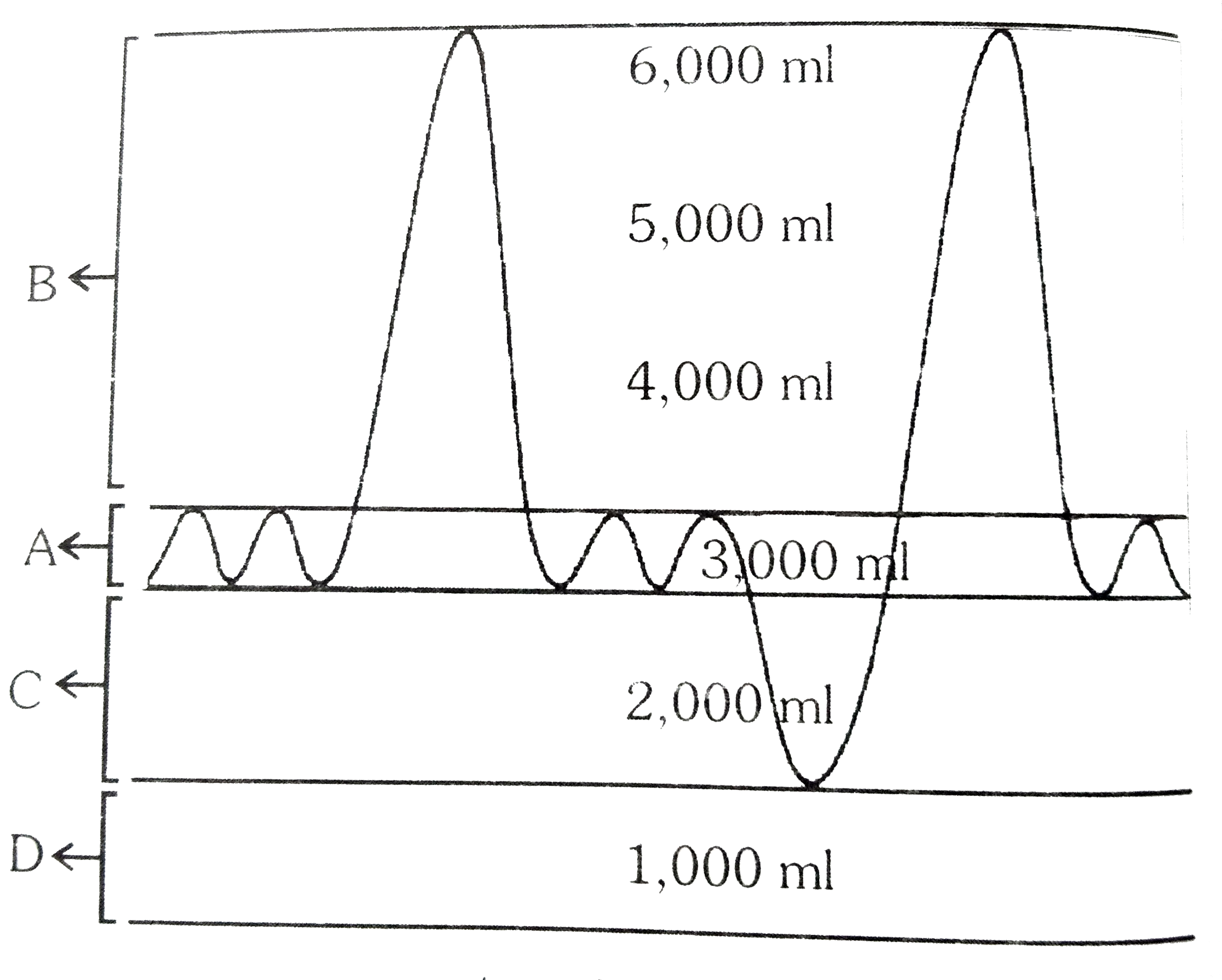
Which represent expiratory reserve volume :−AABBCCDDIdentify the correct and incorrect match abount respiratory volumes and capacities and mark the correct answer :- A. Inspiratory capacity (IC) = TV + RV B. Vital capacity (V.C.) = TV + IRV + ERV C. Residual volume (R.V.) = VC – IRV D. Tidal volume (TV) = IC – IRV
AA, B, C incorrect and D correctBA, C incorrect and B, D correctCA, B, D correct and C incorrectDA, C correct and B, D incorrect
Lung Volumes and capacities
View SolutionRespiratory Volumes and Capacities
View SolutionSelect the correct option about pulmonary volume and capacities
(A) VC=IRV+TV+ERV
(B) FRC=IRV+RV
(C) IC=IRV+TV
(D) EC=ERV + RV
(E) TLC=VC+RV
View SolutionIn the graphical representation of pulmonary Volumes and capacities, 'x' denotes

View Solutionn moles of an ideal gas with constant volume heat capacity CV undergo an isobaric expansion by certain volumes. The ratio of the work done in the process, to the heat supplied is:
View Solution

