Compound interest
Compound Interest
What is Compound Interest?
The process of compounding means growing or developing. In case you're acquainted with the "snowball effect," you realize how something can expand upon itself. Compound interest is interest earned on cash that was previously earned as interest. This cycle leads to increasing interest and record balances at an increasing rate, sometimes known as exponential development.
Understanding Compound Interest?
Before delving into compound interest, let us first explore the idea of simple interest: you deposit some amount in cash, and the bank pays you interest on your deposit.
For instance, on the off chance that you receive 10% yearly interest, a deposit of Rs. 100 would pick up you Rs. 10 following a year. What happens the next year? That is the place exacerbating comes in. You'll procure interest on your initial deposit, and you'll receive interest on the interest you just earned.
In this manner, the interest you gain the second year will be more than the prior year because your record balance is presently Rs. 110, not Rs. 100. So even though you didn't make any deposits, your earnings will increase.
- First Year- An initial deposit of Rs. 100 earns 10% interest, or Rs. 10, carrying your balance to Rs. 105.
- Second Year- Your Rs. 110 earns 10% interest, or Rs. 11; your balance is presently Rs. 121
- Third Year - Your balance of Rs. 121 earns 10% interest, or Rs. 12.10; your balance is presently Rs. 133.10
Compound Interest Formula
To practice the compound interest formula, you will require figures for principal sum, yearly interest rate, time span and the number of compound periods. When you have those, you can determine the compound interest amount.
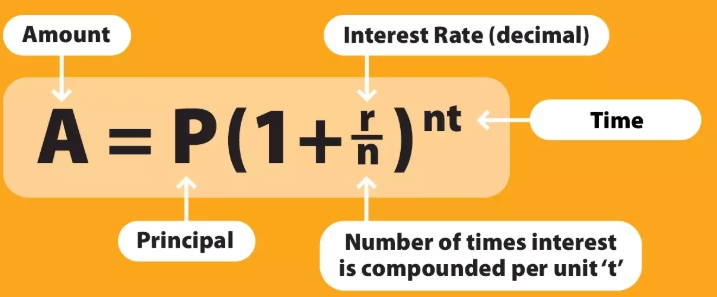
This formula gives you the future estimation of an investment or loan, which is compound interest plus the principal. Should you wish to figure the accumulating funds just, you have to deduct the principal from the result. So, your equation looks this way:
Compound interest just (without principal): P (1 + r/n) (nt) – P
Related Videos:
Solved Questions on Compound Interest
Ques 1: Find the total amount, if Rs 25000 is invested at 12% compounded p.a. for 3 years.
Sol: Using the formula:A= P [1+ R/100]n
A = 25000 [1 + (12/100)]3
On Solving, we get A = Rs. 35123
Ques 2: Find the Compound Interest, if Rs 2000 was invested for 1.5 years at 20% p.a. compounded half yearly.
Sol: It is given that the interest is compounded semi annually. So, time will be doubled and the rate of interest will be halved.
CI = P [1+(R/100)]n - P
CI = 2000 [1+(10/100)]3- 2000
On Solving, we get
CI = Rs. 420
Ques 3: The Compound interest on a amount of Rs 400 in 2 years is Rs 41. Find the rate of interest.
Sol: We know that Amount = Compound Interest + Principal
A = 400 + 41 = 441
Using the formula: A = P [1+(R/100)]n
441 = 400 [1+(R/100)]2
441/400 = [1+(R/100)]2
Since, 441 is the square of 21 and 400 is the square of 20
Therefore, (21/20)2 = [1+(R/100)]2
21/20 = [1+(R/100)]
21/20 - 1 = R/100
On solving, R = 5%
Ques 4: A amount of money is put on compound interest for 2 years at 20%. It would give Rs 482 more if the interest is payable half yearly than if it were payable yearly. Find the principal amount.
Sol: Let the Principal = Rs 100
When compounded annually,
A = 100 [1+20/100]2
When compounded half yearly,
A = 100[1+10/100]4
Difference, 146.41 - 144 = 2.41
If difference is 2.41, then Principal = Rs 100
If difference is 482, then Principal = 100/2.41 × 482
Principal amount = Rs 20000.
Ques 5: Ramesh lended an amount of money at compound interest. It amounted to Rs 2420 in 2 years and Rs 2662 in 3 years. Find the yearly rate percent.
Sol: Final year interest = 2662 - 2420 = Rs 242
Therefore, Rate% = (242 * 100)/(2420 * 1)
Rate% = 10%
Important Note: To find the difference between Simple Interest and Compound Interest for 2 years, we use the formula Difference = P[R/100]2
Ques 6:The difference between Simple Interest and Compound Interest for 2 years @ 20% per annum is Rs 8. Find the principal amount.
Sol: We know the formula: Difference = P (R/100)2
Difference = Rs 8
T= 2 years
Rate= 20%
Putting all values in the above formula,
8 = P[20/100]2
On Solving we get,
P = Rs 200
Therefore, the principal amount is Rs 200
Ques 7: If an amount of Rs. 10,000 is credited into a savings bank account at 5% p.a., compounded monthly, find the value of the principal amount after 10 years.
Solution: P = 10000.
r = 5/100 = 0.05
n = 12.
t = 10.
Putting those values into the formula : P (1 + r/n) (nt),
we obtain the following:
A = 10000 (1 + 0.05 / 12) (12 * 10) = 16,470.09
So, the total amount after 10 years is Rs. 16,470.09
Ques 8 : A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs1600 each on 1st January and 1st July of a year. Find the amount that the customer would have earned through interest at the end of the year.
Sol:
Case 1: Rs1600 deposited on 1st January
Interest for 6 months =12[5%(1600)]=40
Interest for next 6 months =40+12[5%(40)]=41
Total interest =40+41=81
Case 2: Rs1600 deposited on 1st July
Total interest =12[5%(1600)]=40
Required amount gained at the end of the year =81+40=121
Ques 9 : The difference between simple and compound interest(compounded annually) on a certain sum for 2 years at 4% per annum is Rs 1. What is the sum?
Sol:
Let the sum be x
Amount after 2 years (interest compounded annually)
=x(1+4/100)2=x(26/25)2
Compound interest
=x(26/25)2−x
=x[(676/625)−1]
=51x/625
Simple interest =x×4×2/100=2x /25
Difference between compound interest and simple interest is 1
Therefore,
⇒51x/625−2x/25=1
On solving, we get the following,
⇒x=625
Thus, the sum amount is Rs 625
Important Chapters:

A = 25000 [1 + (12/100)]3
On Solving, we get A = Rs. 35123
CI = 2000 [1+(10/100)]3- 2000
On Solving, we get
CI = Rs. 420
A = 400 + 41 = 441
Using the formula: A = P [1+(R/100)]n
441 = 400 [1+(R/100)]2
441/400 = [1+(R/100)]2
Since, 441 is the square of 21 and 400 is the square of 20
Therefore, (21/20)2 = [1+(R/100)]2
21/20 = [1+(R/100)]
21/20 - 1 = R/100
On solving, R = 5%
When compounded annually,
A = 100 [1+20/100]2
When compounded half yearly,
A = 100[1+10/100]4
Difference, 146.41 - 144 = 2.41
If difference is 2.41, then Principal = Rs 100
If difference is 482, then Principal = 100/2.41 × 482
Principal amount = Rs 20000.
Therefore, Rate% = (242 * 100)/(2420 * 1)
Rate% = 10%
Important Note: To find the difference between Simple Interest and Compound Interest for 2 years, we use the formula Difference = P[R/100]2
8 = P[20/100]2
On Solving we get,
r = 5/100 = 0.05
n = 12.
t = 10.
Interest for 6 months =12[5%(1600)]=40
Total interest =40+41=81
Total interest =12[5%(1600)]=40
=x(1+4/100)2=x(26/25)2
=x(26/25)2−x
⇒51x/625−2x/25=1
Knowledge Check
A sum of Rs.15000 is lent at compound Interest (compounded annually) at an interest rate of 20% per annum. If the interest is compounded half yearly, then how much more interest in Rs.) will be obtained in one year?
A225B150C75D300A sum of Rs.15000 is lent at compound Interest (compounded annually) at an interest rate of 20% per annum. If the interest is compounded half yearly, then how much more interest in Rs.) will be obtained in one year?
A225B150C75D300
