Question

Pyramid a pyramid is a solid whose base is a plane rectilinear figure and whose side-faces are triangles having a common vertex outside the plane of the base.

Explanation

Pyramid

A pyramid is a 3-dimensional geometrical figure with a base (any polygon), and three or more triangular sides that meet at a point called the apex. These triangular faces are sometimes called the lateral faces to differentiate them from the base.

Types of Pyramids

There are different types of pyramids, depending on the shapes of their bases.

• Triangular Pyramid


• Square Pyramid


• Pentagonal Pyramid


• Right Pyramid


• Oblique Pyramid

Triangular Pyramid

The base of this pyramid is triangular.

Square Pyramid

As the name suggests, the base of this pyramid has a square shape.

Pentagonal Pyramid

This pyramid has a base of a pentagon shape; therefore, we call it a Pentagonal Pyramid.

Right Pyramid

The apex or pinnacle point of this pyramid is exactly over the centre point of the base.

Oblique Pyramid

The apex or pinnacle point of this pyramid is not exactly over the centre point its base.

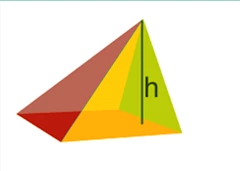
Pyramid Formulae

The pyramid surface area is the total area of all the faces plus base  area, including perimeter and slant height,

Surface Area = (base area) + (1/2) × (perimeter) × (slant height)

To determine the volume of pyramid, the formula is;

Volume = 1/ 3 × (Base Area) × height

Base area is the area of the base of the pyramid, which will change based on its types.

Related Video:

• Quadrilateral pyramid


• Triangular pyramid


• Regular pyramid


• Pyramid – Volume & Surface Area

Volume of Pyramid

The volume of a pyramid depends on the sort of pyramid's base, regardless of whether it is a triangle, square or square shape. The base of the pyramid is a polygon with 3 or more sides. Subsequently, the equation to discover volume, as well as the surface area of a pyramid, depends on the structure of its base and slant height.

Volume of Triangular Pyramid

Since this pyramid has a triangular base.

The area of a triangle;

A = 1/2 base (b) x height (h)

Thus, the volume of a triangular pyramid is,

= 1/3 x Area of base (traingle) x Height of pyramid (H)

V = 1/3 x (1/2 b.h) x H

Volume of Triangular Pyramid = 1 /6 b.h.H

Volume of Square Pyramid

This pyramid has a square shape base.

Since, the area of a square is:

A = s²

Where s is the length of the side of the square.

Thus, the volume of a square pyramid is given by:

Volume = 1/3 x Area of base (square) x Pyramid Height (H)

V = 1/3 x s² x H

Volume of Square Pyramid = 1/3 . s² . H

Volume of Rectangular Pyramid

This pyramid has a rectangular base.

Since, the area of rectangle :

A = Length x breadth

A = l x b

Thus, the volume of a rectangular pyramid will be:

V = 1/3 x A x Height of Pyramid (H)

Volume of Rectangular Pyramid = 1/3 l . b . H

Volume of Hexagonal Pyramid

This pyramid has a hexagonal base.

Volume of pyramid = 1/3 x area of base x pyramid height (H)

Area of hexagonal base = 3√3/2 a²   , a is length of each side of a hexagon

Volume of Hexagonal pyramid = 1/3 x 3√3/2 a² x H

Volume of Hexagonal pyramid = √3/2 a² H

Solved Questions

Q1. Find the volume of a square pyramid. Given, the sides of the base are 20 cm each and the height of the pyramid is 15cm.

Sol: Volume of a pyramid, V = ⅓ A H

The area of the square base is a² = 20 x 20 = 400 cm²

Thus,

Volume of Square pyramid= ⅓ x 400 cm ² x 15 cm

= 400 x 5

V= 2000 cm³

Q 2. Find the volume of a square pyramid. Given, the sides of the base are 10 cm each and the height of the pyramid is 12cm.

Sol: Volume of a pyramid, V = ⅓ A H

The area of the square base is a² = 10 x 10 = 100 cm²

Thus,

Volume of Square pyramid = ⅓ x 100 cm ² x 12 cm

= 100 x 4

V= 400 cm³

Q 3. . Find the volume of a rectangular pyramid having base length 5 cm and the breadth is 8 cm and the height of the pyramid is 15cm.

Sol: Length of rectangular base of pyramid = 5 cm

Breadth of rectangular base of pyramid =  8 cm

and height of the pyramid = 15 cm

Volume of rectangular pyramid,

V = 1/3 l .b . H

On putting the respective values we get;

V = 1/3 x 5 x 8 x 15

V = 600/3

V= 200 cm³

Q 4: The area of the base of a triangular pyramid is 150 cm² and the height of the pyramid is 6 cm. Find the volume of the pyramid

Sol: Area of the base of pyramid =  150 cm²

Volume of Pyramid = 1/3 x A x H

V = 1/3 x 150 x 6

V = 900/3

Volume of the triangular pyramid = 300 cm³

Q5. Find the volume of a square pyramid. Given, the sides of the base are 10 cm each and the height of the pyramid is 12cm.

Sol: Volume of a pyramid, V = ⅓ A H

The area of the square base is a² = 10 x 10 = 100 cm²

Thus,

Volume of Square pyramid= ⅓ x 100 cm ² x 12 cm

= 100 x 4

Volume of square pyramid = 400 cm³

Q6. Find the volume of a triangular pyramid. Given, the area of base is 125 cm² , and height and the height of the pyramid is 12cm.

Sol: Area of the base of triangular pyramid = 115 cm²

Volume of Pyramid = 1/3 x A x H

V = 1/3 x 125 x 12

V = 125 x 4

Volume of a triangular pyramid = 500 cm³

Q 7. Find the volume of a rectangular pyramid having base length 10 cm and the breadth is 6 cm and the height of the pyramid is 12 cm.

Sol: Length of rectangular base of pyramid = 10 cm

Breadth of rectangular base of pyramid =  6 cm

and height of the pyramid = 12 cm

Volume of rectangular pyramid,

V = 1/3 l .b . H

On putting the respective values we get;

V = 1/3 x 10 x 6 x 12

V = 10x 6 x 4

V= 240 cm³

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Class 6 Maths Chapter Understanding Three Dimensional Shapes