Rectangle a parallelogram whose each angle is a right angle is called a rectangle.
Area of a Rectangle
The region which is covered by the rectangle in a two-dimensional plane is known as the area of the rectangle. It happens to be a four-sided polygon where the length of the opposite sides is equal. It is also known as an equiangular quadrilateral because each angle measures 90 degrees. Here, we will discuss the definition of the rectangle as well as the area of a rectangle, properties of a rectangle, and so on. This would make it possible to get a clear idea about it.
Definition of Rectangle
A rectangle is also termed as a parallelogram as the opposite sides are parallel and equal, but with each angle equal to 90 degrees. On the other hand, if all its sides are of equal length, then it is called a square.
Formula for the Area of a Rectangle
When it comes to the measurement of the size of any object, it is possible in different ways. Suppose, we try to make a calculation as to what is the size of a swimming pool or how tall the building is, and so on. So, you might be confused as to what is the area of a rectangular object. Therefore, here, we will find out the area of a rectangle.
The area of a rectangle is determined by multiplying the breadth (or width) by the length of a rectangle. In the case of three-dimensional figures, the calculation is done for lateral and total surface areas. Because of being a two-dimensional figure, it is not possible to calculate for the rectangle. So, in this case, the formula for perimeter as well as the area of a rectangle can be seen as under:
The formula for the Area of a Rectangle
Perimeter of a Rectangle
P= 2(l + b)
Area of a Rectangle
A = l × b
If the length and width of any rectangle are known, then it is possible to calculate its area. The area of the rectangle would be obtained by multiplying the length and breadth, and the area would be in square-units dimension. The area will become length2 in the case of a square. Coming to the major difference between rectangle and square is that the breadth and length are equal for square.
Related Videos:
- Each of the four angles of a rectangle is a right angle
- Angle bisectors of a parallelogram form a rectangle
- Each angle of a rectangle is a right angle
Step by step process to calculate the area of a Rectangle
You need to follow the below steps to find the area:
- You need to take in consideration of the dimensions of the length and width from the given data.
- Next you have to multiply the values of the length and width
- Now you need to write the answer in square units
Find below the special formula that is related to the rectangle area
In order to find the area with diagonal of the width of a rectangle, it is given below:
Area = 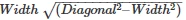
To find a missing side length when you know the area, then you can use:
Length = Area/Width
Example of Area of Rectangle
Example 1: Can you find the area of the rectangle whose length is 25 cm and the width is 4 cm?
Solution:
Given,
Length = 25 cm
Width = 4 cm
Area of a rectangle = Length × Width
25 × 4 = 100
So the area of rectangle = 100 cm2
Example 2: Find the area of the rectangle whose length is 30 cm and the width is 5 cm?
Solution:
Given,
Length = 30 cm
Width = 5 cm
Area of a rectangle = Length × Width
30 × 5 = 150
So the area of rectangle = 150 cm2
Example 3: Can you calculate the area of a rectangular blackboard whose length and breadth are 140 cm and 100 cm respectively.
Solution:
The length of the blackboard = 140 cm = 1.4 m
Now breadth of the blackboard = 100 cm = 1 m
Area of the blackboard = area of a rectangle = length x breadth = 1.4 m x 1 m = 1.4 square-metres
Example 4: Can you calculate the area of a rectangular blackboard whose length and breadth are 200 cm and 120 cm respectively.
Solution:
Length of the blackboard = 200 cm = 2 m
Breadth of the blackboard = 120 cm = 1.2 m
Area of the blackboard = area of a rectangle = length x breadth = 2 m x 1.2 m = 2.4 square-metres
Perimeter of a Rectangle Formula
The sum of all sides of a rectangle is known as the perimeter of a rectangle. The total distances around its sides are the perimeter formulas for any polygon. If it is a rectangle, then it proves to be equal when it comes to the opposite sides of a rectangle. It is denoted by the letter, ‘p.’
Take for example, that a rectangle has length and width as a and b respectively.
We come to know from the definition that the perimeter of a rectangle, p = 2 (a + b) units where
‘a’ happens to be the length of the rectangle and
‘b’ happens to be the breadth of the rectangle
Derivation
As we know that the sum of all the sides of the polygon is its perimeter, therefore, the perimeter (P) in case of a rectangle is:
P= Sum of all the four sides
P = a + b + a + b
(P = 2 (a + b)
Hence, derived
Therefore,
We can take Perimeter of a rectangle = 2(Length + Width) square unit
If we happen to write the formula for the area of a rectangle in accordance with the figure provided then
Area of a rectangle = Length × Width = a × b
Problem 1
A rectangle has got a length and width of 8 cm and 12 cm, respectively. Find the perimeter.
Solution:
Given:
Length = 8 cm and Width = 12 cm
We know that,
The perimeter of a rectangle = 2 (length + width)
Now by substituting the value of length and width, we get
Perimeter, P = 2(8 + 12) cm
P = 2 x 20 cm
Therefore, the perimeter of a rectangle = 40 cm
Problem 2
A rectangle has a length and width of 10 cm and 14 cm, respectively. Find the perimeter
Solution:
Given:
Length = 10 cm and Breadth = 14cm
As we know,
The perimeter of a rectangle = 2(length + width)
By substituting the value of length and width, we get
Perimeter, P = 2(10 + 14) cm
P = 2 x 24 cm
Therefore, the perimeter of a rectangle = 48 cm
Problem 3:
Can you find the width of a rectangular yard that has got length which is equal to 20cm and perimeter equals to 80?
Solution:
Given,
Perimeter of the yard = 80cm
Length of the yard = 20cm
By using the formula, we find,
Perimeter, P = 2(length + width)
Now after including the value, we get;
80 = 2(20 + width)
20 + W = 40
W = 40-20=20
Therefore, we find that the width of the yard is 20 cm.
Important Chapters:
The formula for the Area of a Rectangle
Perimeter of a Rectangle
P= 2(l + b)
Area of a Rectangle
A = l × b
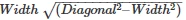
Similar Questions
Right triangle a triangle whose one angle is a right angle is called a right-angled triangle or a right triangle.
View SolutionIn a parallelogram if each angle is equal then it is called a
View SolutionA quadrilateral whose each angle is a right angle is a square (b) rectangle rhombus (d) parallelogram
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View SolutionProperty 1 each angle of a rectangle is a right angle.
View SolutionRIGHT TRIANGLE A triangle whole one angle is a right angle is called a right-angled triangle or right triangle.
View SolutionShow that each angle of a rectangle is a right angle.
View SolutionEach angle of a rectangle is a right angle.
View SolutionShow that each angle of a rectangle is a right angle
View SolutionUsing dot product of vectors; prove that a parallelogram; whose diagonal are equal; is a rectangle.
View Solution
