Question

Perimeter of a triangle the sum of the lengths of the sides of a triangle is called its perimeter.

Explanation

Perimeter of a Triangle

In this chapter, we would discuss the perimeter of a triangle. We will also focus on the perimeter of a triangle formula. To make things clearer and much easier, we will work on different problems.

What is the Perimeter of a Triangle?

The perimeter of any closed shape can be calculated by adding the length of each of the sides. In the case of a triangle:

Perimeter = sum of the three sides. It is important to include units in the answer. If centimeters are given in the sides of a triangle, then the answer should also be in centimeters. 

What is the Perimeter of a Triangle Formula?

When it comes to the perimeter of a triangle formula of a closed shape figure, then it is usually equal to the length of the outer line. The perimeter will be the sum of all the three sides in case of a triangle. For example, if the three sides of a triangle is a, b and c then,

Perimeter, P = a + b + c

Perimeter of an Isosceles, Equilateral and Scalene Triangle

To understand the perimeter of an Isosceles, Equilateral and Scalene Triangle, you need to look at the figures below:

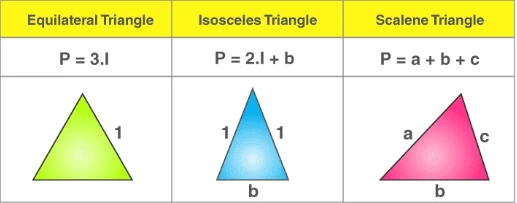
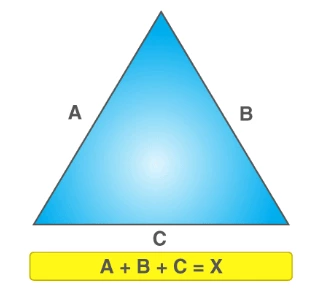
Here P = perimeter and a, b, c and l are the side lengths. You need to add the lengths of all its 3 sides together. If the side measures are A, B and C and X is the perimeter then

What is the Perimeter of Right Triangle?

There is base (b), perpendicular (p) and hypotenuse (h) in a triangle as its sides. So, according to Pythagoras theorem, we have

h² = b² + p²

So, the perimeter of a right angle triangle = b + p +h

Perimeter, P = b + p+ √ b² + p²

Related Videos:

• Sides of a Triangles


• Interior of Triangles


• Exterior of Triangles


• Altitudes of the triangle


• Triangular Region

We will now focus on some examples to get a fair idea about it

Problem 1: A triangle has sides of 4 cm, 9 cm and 6 cm. Find the perimeter.

Solution:  Perimeter of a triangle

                   = sum of all the three sides

                   = AB + BC + AC

                   = 4 cm + 9 cm + 6 cm

                   = 19 cm

Problem 2: The length of three sides of a triangle are 4 cm, 6 cm, 10 cm. Find the perimeter.



Solution:   Perimeter of a triangle

                  = Sum of all the three sides

                  = 4 cm + 6 cm + 10 cm

                  = 20 cm

Problem 3: The perimetеr of an isosceles triangle is 37 centimetres along with a base of length 9 centimetres. Can you find the length of each of the other two sides?

Solution: In an isosceles triangle, the two sides are equal.

Hence, 37 – 9 = 28 cm

Therefore, the length of each of the other two sides is 14cm.

Problem 4: Jimmy builds a square where the side measures 12 cm from some wire. If he decides to build a rectangle from the same wire with a width of 6 cm, find the length of the rectangle?

Solution: Here, the side of the square = 12 cm

The perimeter would be = 48 cm

Width = 6 cm

Therefore, length of the rectangle = (48-12) ÷ 2 = 36 ÷ 2 = 18 cm

Problem 5: The perimeter of a triangle is 40 cm, and two sides are 10 cm each? Can you find the missing side length of the triangle?

Solution: Given,

Perimeter = 40 cm

Here, the length of two sides are same i.e. 10 cm, is an isosceles triangle.

By using formula: P = 2l + b

40 = 2 * 10 + b

40 = 20 + b

or b = 20

So, missing side length is 20 cm.

Problem 6: A park has the shape of a rectangle. The length of the park is 24 meters along with a width of 18 meters. If there is a decision made to plant trees on its sides with gaps of 2 meters between them, can you calculate as to how many trees would be required?

Solution: Here, the perimeter of the rectangle is:

            2 × (24 + 18)

            We get, 2 × 42 = 84 meters

            So, the number of trees required would be 84 ÷ 2 = 42 trees.

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 6 Chapter Understanding Elementary Shapes


• NCERT Solution for Maths Class 7 Chapter The Triangle And Its Properties


• NCERT Solution for Maths Class 7 Chapter Congruence Of Triangles