Equilateral triangle a triangle whose all sides are equal to one another is called an equilateral triangle.
Equilateral Triangle
This chapter focuses on the equilateral triangle and on the area of equilateral triangle formula, equilateral triangle properties,. When all sides of the triangle are equal in length, it is known as an equi
lateral triangle. Here, the meaning of ‘equi’ is equivalent, and ‘lateral’ means sides. You should also remember that it is called an equiangular triangle. It is also a type of regular polygon that has three equal sides where it is also termed as a regular triangle.
What are the properties of an equilateral triangle?
It is to be noted that an equilateral triangle is a special case of the isosceles triangle where there is also equal in the third side. So, it is important to remember that in a triangle ABC, AB = BC = CA. Now looking at the equilateral triangle properties, here it goes:
- A triangle in which all three sides are equal is an equilateral triangle
- Equilateral triangles prove to be equiangular. This means that all three internal angles are also equal, where the only value possible is 60 degree each.
- It is also a regular polygon with 3 sides.
- If any three of the smaller triangles have either the same perimeter or the same in radius, then a triangle is said to be equilateral.
- The amount of space which is occupied by an equilateral triangle is the area of an equilateral triangle.
- The perimeter of an equilateral triangle is 3a.
- The perpendicular, angle bisector and the median in an equilateral triangle are all the same.
- The centroid and ortho-centre of the triangle happen to be the same point.
- The area of an equilateral triangle is equal to √3 a2/ 4
What is meant by area of an equilateral triangle?
The space that it occupies in a 2-dimensional surface is known as the area of an equilateral triangle. So, here the area of equilateral triangle formula is given by:
A = (√3/4) a2
Here, the length of sides = a
How to derive the Area of Equilateral Triangle?
In order to derive the formula for the area of equilateral triangles there are three methods which are:
1) Using the basic triangle formula: This is done by taking an equilateral triangle of the side ‘a’ units. After this, a perpendicular bisector is drawn to the base of height ‘h’.

Now,
Area of Triangle = ½ × base × height
Here, height = h and base = a,
Now, by applying Pythagoras Theorem, we find
a2 = h2 + (a/2)2
⇒ h2=a2–a2/4
⇒ h2=(3a2)/4
Or, h=½(√3a)
Now, by putting the value of “h” in the area of the triangle equation,
We get
Area of Triangle = ½ × base × height
⇒ A = ½ × a × ½(√3a)
Or, Area of Equilateral Triangle = ¼(√3a2)
2) Using rectangle construction: Let us assume an equilateral triangle that have sides which are equal to ‘a’.
Now, from the top triangle vertex to the midpoint of the base of the triangle, we will drop a straight line where it would divide the base into two equal halves.

Now the straight line is cut along and then the other half of the triangle is moved to form the rectangle.
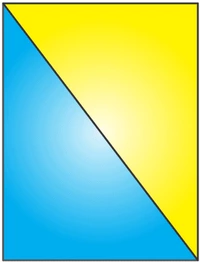
Here, ‘a’ is considered to be the length of the equilateral triangle and ‘h’ is the height
The area of an equilateral triangle is equal to area of a rectangle = ½×a×h …………. (i)
From the figure above, it can be seen that half of the rectangle is a right-angled triangle.
Therefore, by applying the Pythagoras Theorem, we get
⇒ a2=h2+ (a/2)2
So, h2=(3/4)a2
Therefore h = (√3/2)a …………..(ii)
Now, we will substitute the value of (ii) in (i), where we get:
Area of an Equilateral Triangle
=(½)×a×(√3/2)a
=(√3/4)a2
3) Using trigonometry: The height can be calculated using trigonometric functions provided the two sides of a triangle are given. Therefore,, the height of a triangle ABC will be-
h = b•Sin C = c•Sin A = a•Sin B
Here, we find that the area of ABC = ½ × a × (b • sin C) = ½ × b × (c • sin A) = ½ × c (a • sin B)
Since it is a equilateral triangle, a = b = c = 60°
Area = ½ × a × (a • Sin 60°) = ½ × a2 × Sin 60° = ½ × a2 × √3/2
So, Area of Equilateral Triangle = (√3/4)a2
Related Videos:
It is very important to work on some problems to get the perfect idea about it. We will try to have a look at it in the best way.
Problem 1: Can you find the area of the equilateral triangle ABC, where AB=AC=BC = 4cm?
Solution:
By the formula, we know;
Area = √3a2/4
Given a = 4cm
Hence, by putting the value we get;
Area = √3(4)2/4
A = 4√3
Problem 2: Find the altitude of an equilateral triangle whose sides are equal to 10cm.
Solution:
By the formula we know,
Altitude of equilateral triangle = √3a/2
Since, a = 10cm
Hence,
h = √3 x (10/2)
h = 5√3
Question 3: What is the area of an equilateral triangle of perimeter 45 cm?
Solution: If we consider the side of the equilateral triangle as ‘a’, its perimeter P will be given by
P = 3
= P / 3 = 45 / 3 = 15 cm
Area A = 225√3cm 2
4
Question 4: What is the area of an equilateral triangle of height 20 units?
Solution: If ‘h’ is considered to be the height of the equilateral triangle and ‘a’ as its side, then we have the relationship
h = a√3
2
h = 20, hence the equation: 20 = a 40
√3
Now, we solve for a to get: a=40
√3
Hence, Area A = a2√3
= (40)2–√3 =400 √3 unit2
√3 4 3
Question 5: Can you find the area of the circumscribed circle of an equilateral triangle of side a = 5 inches?
Solution: Let us assume R be the radius the circumscribed circle to an equilateral triangle of side a, then , we can find
R = a√3 = 5√3 where a=5 given
3 3
Therefore, Area of circle of radius R = πR2= π (5√3)2 = 25 π inches2
3 3
Question 6: Find out the radius of the inscribed circle of an equilateral triangle with an area of 100 cm2
Solution: Let u assume that r is the radius of the inscribed circle to an equilateral triangle of side a, then we can find,
r = a√3
6
Now, we square both sides of the above to get: r 2 = a2
12
Area A of circle of radius r is given by: A = πr2= πa2
12
Now, the area of the equilateral triangle is given, hence: 100 = a2 √3/4
Now, we solve the above to find: a2= 400/ √3
Next, by substituting a 2 found above into the expression of the area A = πa2 /12
So, we now find that:
400
A = π √3
12
= π 100√3 cm2
9
Important Chapters:




P = 3
= P / 3 = 45 / 3 = 15 cm
h = a√3
h = 20, hence the equation: 20 = a 40
R = a√3 = 5√3 where a=5 given
Therefore, Area of circle of radius R = πR2= π (5√3)2 = 25 π inches2
r = a√3
6
Area A of circle of radius r is given by: A = πr2= πa2
Now, the area of the equilateral triangle is given, hence: 100 = a2 √3/4
Now, we solve the above to find: a2= 400/ √3
Similar Questions
Knowledge Check
STATEMENT-1 : The points (2, 3, 5), (7, 5, 7) and (-3, 1, 3) are vertices of an equilateral triangle.
and
STATEMENT-2 : The triangle with equal sides is called an equilateral triangle.AStatement-1 is True, Statement-2 is true, Statement- is a correct explanation for Statement -1BStatement-1 is True, Statement-2 is true, Statement- is NOT a correct explanation for Statement -1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is trueIn the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
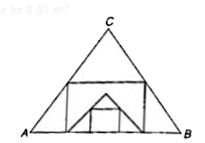 Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of these
Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of theseWhat is the ratio of side to the height of an equilateral triangle?
A2:1B1:1C2:√3D√3:2
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionProve that area of an equilateral triangle formed on one side of a given square is one half of area of equilateral triangle formed on diagonal is the same square.
View SolutionA triangle whose all sides are equal is called an equilateral triangle (b) an acute triangle a right triangle (d) an isosceles triangle
View SolutionAn equilateral triangle is drawn by joining the midpoints of the sides of another equilateral triangle. A third equilateral triangle is drawn inside the second one joining the midpoints of the sides of the second equilateral tringle, and the process continues infinitely. Find the sum of the perimeters of all the equilateral triangles, if the side of the largest equilateral triangle is 24 units.
View SolutionThere is a vegular hexagon and equilateral triangle inside a circle . If the side of the hexagon is a and side of equilateral triangle in b.Find the relation between a and b.
View Solution
