Question

Length of a line segment

Explanation

Length of a Line Segment

In this chapter, we will discuss the topic that is one of the basic in the field of geometry. Geometry is one of the subjects that take into consideration the line segments, rays and other structures into consideration. In geometry, we can calculate the distance in a given plane surface. One of the most significant components of geometry is the line segment. This is the main component to draw any structure in a given plane and also calculate the averages.

Here, in this chapter, we will focus on the length of a line segment. We will try to understand the line segment formula as well as look at some of the line segment example as well so that you can get a good and clear idea about it.

What is Line Segment?

The line segment is a line that is bounded on two sides by two distinct points. It is a part of the line that connects two points in a plane. In a place when we draw a line, it does not have an endpoint; it can go until infinity. But a line segment will have two definite endpoints so it will have a starting point and an endpoint as well and in many shapes but the most common among them are line segments. When we speak about the curves, other than every other structure in geometry will require a line segment to draw it. 

                        

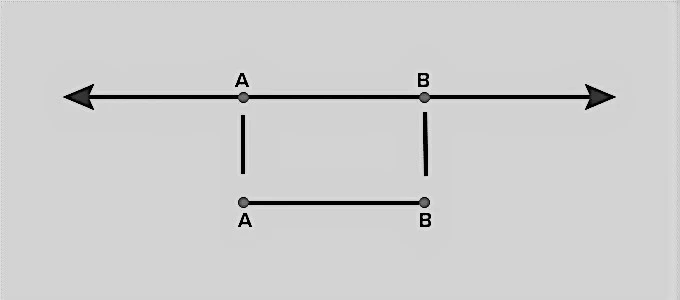
It can also be defined as the shortest distance between two points. In this diagram, as we can see, A and B are two points. So typically, a piece of something that will join these two points is called a line segment. The line segment is always measurable, but its width will always be equal to zero. The length here can be measured in centimetres, millimetres or by any conventional unit of measurement. So here we can see that a closed line segment will definitely have two endpoints. But a line segment that has only one endpoint is called a half-open line segment.

Measurement of Line Segment

As we were discussing above, every line segment has a definite length that can be measured. There are, however, few ways by which this measurement can be carried out.

By Observation

Sometimes, just by observing and comparing two-line segments, we can define the length of the line segment. This is sometimes called predictive measurement as through this method; we will not be able to give the exact measurement in units.

                                     

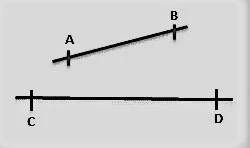
In the above figure, just by looking at it, we can say that line CD is longer than AB. But we cannot say its actual measurement in this case.

Using Trace Paper

The most common method that is used in measuring a line segment is through trace paper. In this method, we can trace one line in a trace paper and place the tracing over the other line. This will give is a better idea as to which one of the lines is larger. This method is more dependent on accuracy as without that proper measurement cannot be done. This can be also said to be one of the methods of observation only because of the reason we cannot give the exact measurement of the line.

Ruler and Divider

This is the most modern and accurate method to measure a line segment. In the ruler, as we can see, the units are marked and well defined. So, placing it over a line segment helps us to get the exact measurement of the same. This ruler and divider method help us to draw a line to the exact decimal point with precision.

So, say we want to measure a line segment, we have to place the ruler set at zero at the beginning of the line segment, and then we will mark the point where the segment ends. This will give us the most accurate measure of the line segment. This happens to be one of the most accurate and reliable methods for measurement.

Related Videos:

• Line


• Naming a line


• Intersecting and parallel lines


• Collinear Points


• Two lines in a plane either intersect at exactly one point or are parallel

Line Segment Formula

There is a definite way that we can measure a line segment using a definite formula. As defined, the line segment has a definite point that it joints. So, say for example we have a line segment have two points in between the endpoints of the line segment. So, when we add up all these points, we will get the actual length of the line segment.

There is also a definite process that can be used to have a perfect measured line segment. This can be done with the help of a compass and a ruler.

• First of all, let us draw a line segment without any length measurement in the plane surface


• Let us mark a point D in the line and assume it as the star of the line segment.


• Now, using the ruler, we can define any length that we want and mark another point say E into the line. This will be the endpoint.


• Now let us measure the distance between D and E in the ruler say the length is 8 cm.


• Now we need to place the compass at the start pint D and mark an Arc in 8 Cm that will coincide with point E.


• So, here we have a line segment DE that has two endpoint D and E.

So, here we have devised out a method where a line segment can be drawn using an exact measurement. The line segment is also termed as the baselines for any geometrical figure. Let is try and see how to make a measurement.

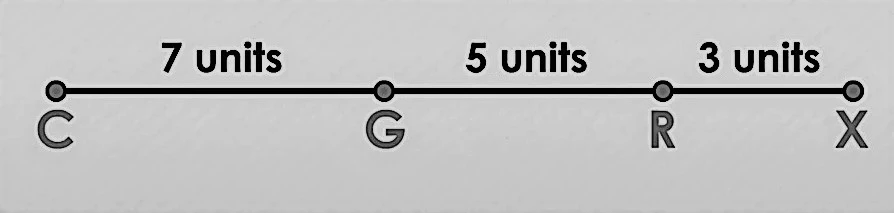
Let us take this example here where we have a line segment with endpoint C and X. Two more points are inscribed at G and R. 

The distance between CG = 7 units, GR = 5 units and RX = 3units

So, if we have to find the total distance of the line segments

CX = CG + GR + RX = 7 + 5 + 3 units

= 15 units

Thus, it gives us a perfect example as to how the length of the line segment can be calculated. So, we can see that in geometry, the line segments are the most important factors that are to be taken into consideration. The line segment gives us the exact distance calculation in a plane dimension. The detailed study of this will have greater importance when we study the structures in geometry.

Important Chapters:

• NCERT Solutions for Maths


• NCERT Solution for Class 6 Maths Chapter Basic Geometrical Ideas