Line
Line
In this chapter, you will learn different concepts on the topic line. Well, the most practical branch of mathematics is the geometry that deals with sizes and shapes of figures along with their properties. It happens to be one-dimensional where it has got length without any height or width. It also extends forever in both directions as well. It is to be noted that when it comes to a 2D plane, the two points can be placed anywhere. There are also different types of lines that are categorised where we will learn here in detail. We will have a look at the topic line in geometrical maths in the best way.
What is a line?
The straight set of points that has no thickness and that extends in both directions is called a line. It is also one-dimensional. Let’s look below.

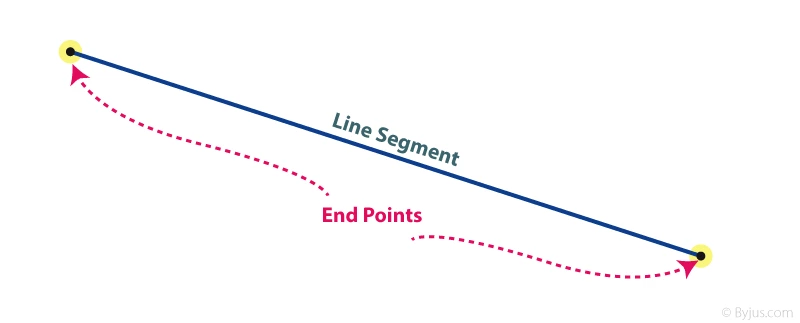
Line Segment
A line segment is the part of a line that has got a starting point and an ending point. Here, you can look below:
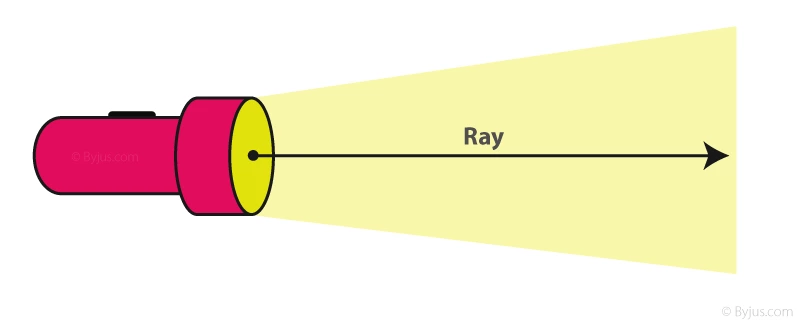
Ray
It is a part of a line that consists of one endpoint, which is a starting point. It should be noted that it extends endlessly in one direction. You can find the right idea about ray by looking below:
Number Line
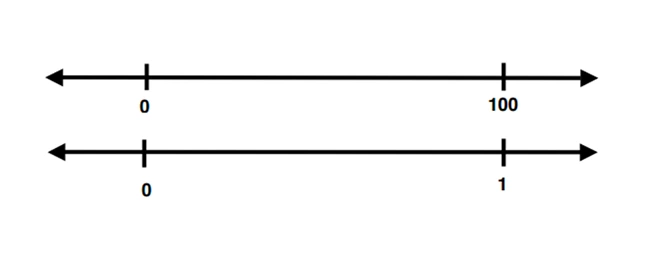
Coming to the number line, it mainly supports the student’s informal thinking strategies. This is due to its inherent linearity. Marks on a number line are naturally recognised by the young children. They recognise it as visual representations of the mental images which are found in most people when they learn to count and also understand the number of relationships. You can look at the below figure to understand the difference between an open number line and predetermined markings and scale of a ruler.
An open number line

An open line helps in allowing students in subdividing, partitioning the space as they see fit. It could be a starting point where you can find below. There is a distance from 0 to 1 or even the distance from 0 to 100. When there is an identification made on the second point of a number line, it moves from an open number line to a closed number line.
Closed number lines
A ray is a line that has one endpoint, and it goes on continuing in one direction. It is also non-terminating for which it is not possible to measure the length of the line.
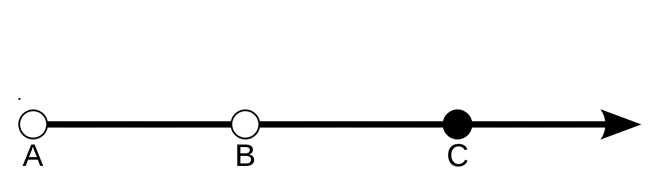
By making use of the starting point and one other point, a ray can be named. In the above figure, you can find a ray AC or BC ray. We can try to name a ray with the use of a lowercase letter ‘r.’
What are the types of line?
There are basically four types of lines in Geometry. Let us have a look at it:
- Horizontal Lines: Horizontal lines move from left to right direction.
- Vertical Lines: Vertical lines run from top to bottom.
- Parallel Lines: Parallel lines are two lines that don’t meet each other at any point, even at infinity.
- Perpendicular Lines: Perpendicular lines are two lines that meet each other at an angle of 90 degrees which are perpendicular to each other.
Related Videos:
- Point
- Naming a line
- Plane
- Intersecting and parallel lines
- Collinear Points
- Two lines in a plane either intersect at exactly one point or are parallel
What are the other types of Lines?
1. Tangent lines: The straight line that just touches the curve at a given point is called the tangent. When it comes to calculating the equation of these lines, the equation of a straight line passing through the point with coordinates (x1, y1) is used where the gradient m is given by:
y – y1 = 1
x – z1
If two lines are with gradients m1 and m2 respectively are found to be perpendicular, then it is given by m1m2 = -1
We will try to make the concepts cleared with line example
Example: Suppose we wish to find points on the curve y(x) given by x3–6x2+x+3. Here the tangents are parallel to the line y = x + 5.
Solution: Given that the tangents are parallel to the line which means that they must have the same gradient. When we apply the standard quotation for a straight line, we have y = mx + c. Here the gradient is ‘m.’ So, m is equal to 1 when we compare it with straight line y = x + 5. Thus, we need to find the gradients of the tangents, which must also have gradient 1.
It is known that if y(x) is differentiated, then an expression can be obtained for the gradients to y(x) where it is possible to set this equal to 1. Now, if we differentiate and set this equal to 1, then we get:
dy/dx = 3x2 – 12x + 1=1
from which
3x2 – 12x = 0
So, what we get is a quadratic equation where you can make use of factorisation in order to solve it:
3x2 – 12x = 0
3x(x -4) = 0
3x = 0 or (x – 4) = 0
x = 0 or x = 4
Therefore, we have found these two values of x where it can be possible in calculating the corresponding y coordinates. Now, we can work on the equation:
y = x3 – 6x2 + x + 3
taking x = 0, y = (0)3 – 6(0)2 + 0 + 3 = 3
taking x = 4, y = (4)3 – 6(4)2 + 4 + 3 = -25
So, we can find that the two points are (0, 3) and (4, -25)
Therefore the gradients of the tangent are equal to 1 from these two points, i.e. y = 5.
2. Secant lines: If a line meets the circle in exactly two points, then the line in the plane is a secant line. It is to be noted that it is also equivalent to the slope between two points or the average rate of change.
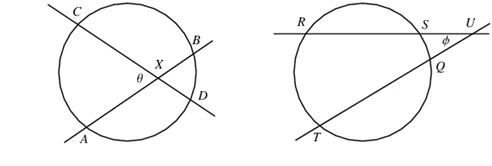
Consider the above figure on the left where we find:
θ = ½ (arc A C + arc B D),
Now, consider the above figure on the right where we find:
ϕ= ½ (arc R T + arc S Q)
Where arc AB denotes the angular measure of the arc AB.
Important Chapters:







