किसी रैखिक प्रोग्रामन की समस्या में उद्देश्य फलन z=3x+8y का अधिकतमीकरण होना है और इसका सुसंगत क्षेत्र एक उत्तल बहुभुज से परिबद्ध है जिसके कोने (0,3), (5,4), (8,0) और (0,0) है | z का अधिकतम मान होगा
52
47
24
64
The correct Answer is:B
Step by step video, text & image solution for किसी रैखिक प्रोग्रामन की समस्या में उद्देश्य फलन z=3x+8y का अधिकतमीकरण होना है और इसका सुसंगत क्षेत्र एक उत्तल बहुभुज से परिबद्ध है जिसके कोने (0,3), (5,4), (8,0) और (0,0) है | z का अधिकतम मान होगा by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- रैखिक प्रोग्रामन BOOK - DAS GUPTACHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्नावली 1B
12 Videos
- यौगिक और प्रतिबंधी प्रायिकता BOOK - DAS GUPTACHAPTER - यौगिक और प्रतिबंधी प्रायिकता EXERCISE - प्रश्नावली 3
16 Videos
- रोले का साध्य एवं लैग्रांजे का मध्य मान सांध्य BOOK - DAS GUPTACHAPTER - रोले का साध्य एवं लैग्रांजे का मध्य मान सांध्य EXERCISE - विविध वस्तुनिष्ट प्रश्न
30 Videos
Similar Questions
एक विक्रेता कुछ पंखे और सिलाई मशीन खरीदना चाहता है उसके पास मात्र 5760 रू. निवेश करने को है और अधिकतम 20 वस्तुओ को रखने की जगह है एक पंखे का मूल्य 360 रू. और सिलाई मशीन पर मूल्य 240 रू है उसे आशा है कि वह एक पंखे को 22 रू के लाभ पर और एक सिलाई मशीन को 18 रू के लाभ पर बेच सकता है यह मानते हुए कि वह खरीदा हुआ सब सामान बेच सकेगा, वह अपने घन को किस प्रकार निवेशित करे कि उसे अधिकतम लाभ मिले ? आलेखित विधि से हल करें एवं अधिकतम लाभ निकाले ।
View Solutionएक व्यक्ति एक सिक्के को 3 बार उछालता है।
एक शीर्ष आने की,
View Solutionयदि f(x)=logx, तो निम्नलिखित में कौन असत्य है ?
View Solutionबताइए कि दिए हुए कथन सत्य हैं या असत्य
किसीLPPकासुसंगतक्षेत्रसदैवएक.....बहुभुजहोताहै∣∣
View Solutionनिचे दिए गए कथन सत्य है या असत्य ?
किसी रेखीय प्रोग्रामन समस्या के लिए संभाव्य क्षेत्र हमेशा रैखिक बहुभुज होता है।
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
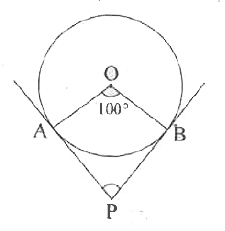
View Solutionसुसंगत क्षेत्र में बिंदु जो उदेश्य फलन का इष्टतम मान (अधिकतम या न्यूनतम ) एक देता है, वह कहलाता है -
View Solutionनिम्न प्रमेय को समझाइए।
प्रमेय 1. यदि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र है तथा उद्देश्य फलन Z=ax+by है। जब Z के एक इष्टतम मान ( अधिकतम या न्यूनतम ) हो जहाँ व्यवरोधों से सम्बंधिर चर और y रैखिक समीकरणों द्वारा व्यक्त हों तब इस इष्टतम मान सुसंगत क्षेत्र के कोनों (शीर्षों )पर होता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
रैखिक प्रोग्रामन समस्या को हल करने के लिए निम्न चरण प्रयुक्त होते हैं -
सुसंगत क्षेत्र के प्रत्येक कोनीय बिंदु पर उद्देश्य फलन Z=ax+by का मान ज्ञात करते हैं। यहाँ से उद्देश्य का न्यूनतम / अधिकतम मान प्राप्त करते हैं।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionउद्देश्य फलन z=x+2y को अधिकतम करने की समस्या का हल प्रतिबंधों x−y≤2,x+y≤4 तथा x,y≥0 के अंतर्गत है -
View Solutionc∈R का अधिकतम मान, जिसके लिए रेखिक समीकरण निकाय x−cy−cz=0,cx−y+cz=0,cx+cy−z=0 का एक अत्युच्च हल है, है
View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
View Solutionरैखिक प्रोग्रामन समस्या मे परिबद्ध व अपरिबद्ध हल क्षेत्र
View Solutionयदि '+' का अर्थ है '+', 'x' का अर्थ है '+',’-’ का अर्थ है 'x’ और ‘+’ का अर्थ है ‘-’ तब निम्नलिखित में से कौन-सा समीकरण सही है?
View Solutionगतिक साम्य में दोनों दिशाओं में अभिक्रिया एक ही दर से होती है और साम्य के दोनों ओर द्रव्यमान किसी भी परिवर्तन से नहीं गुजरता है। यह अवस्था केवल तभी प्राप्त की जा सकती है जब ΔGका मान
View Solution
