An object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s
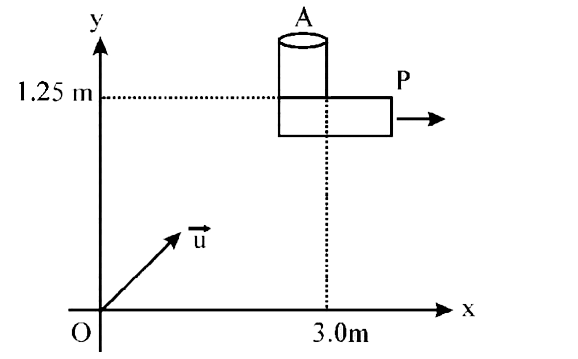
The correct Answer is:u=7.29ms−1,t=1s
Let 't' be the time after which the stone hits the object and θ be the abgle which the velocity vector →u makes with horizontal. According to question, we have following three conditions.
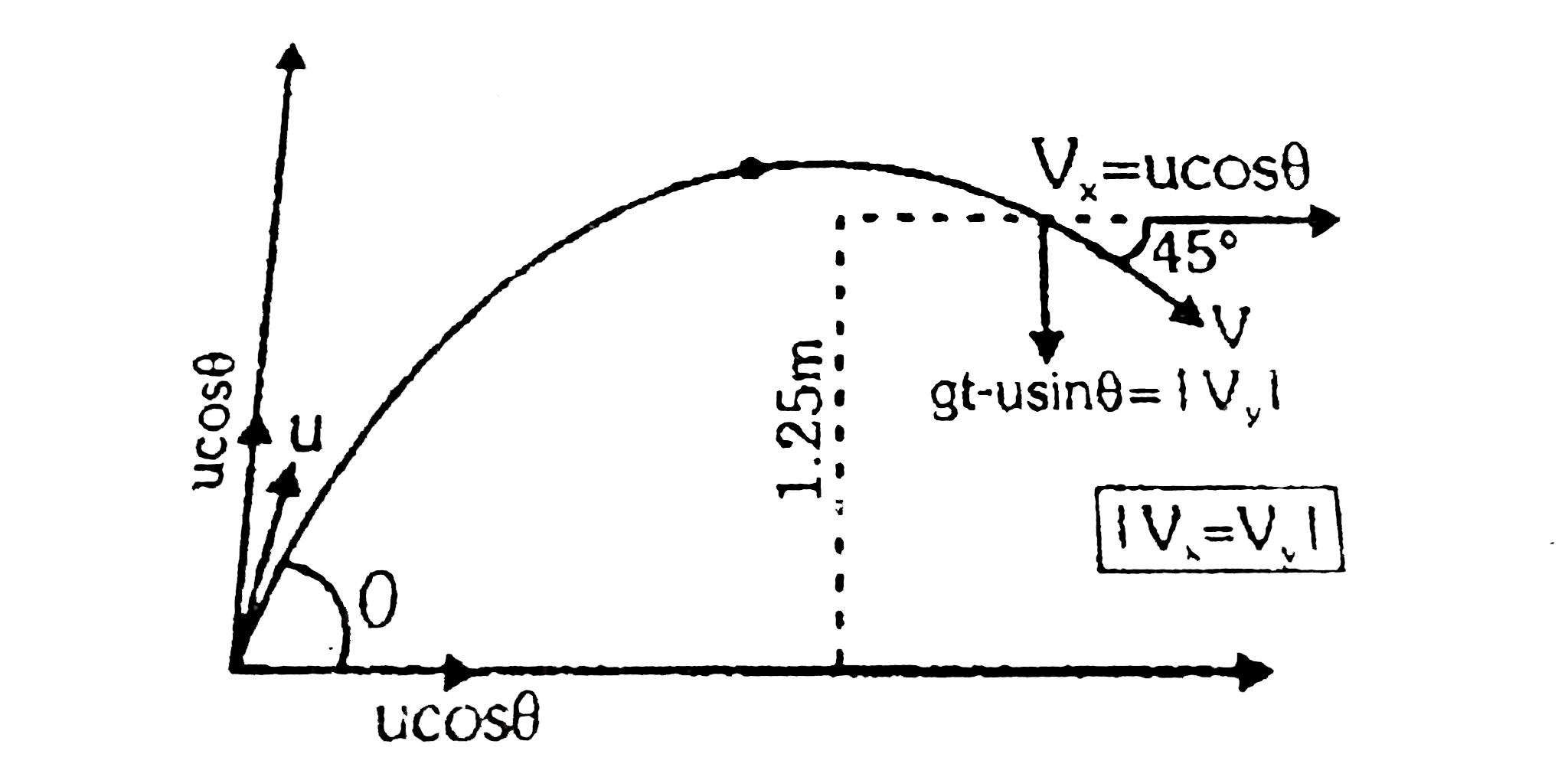
(i) Vertical displacement of stome is 1.25m
∵1.25=(usinθ)t−12gt2 where g=10m/s2
⇒(usinθ)t=1.25+5t2 ...(i)
(ii) horizontal displacement of stone
=3+ dispplacement of object A.
Therefore (ucosθ)t=3+12at2
where a=1.5m/s2⇒(ucosθ)t=3+0.75t2 ...(ii)
Horizontal component of velocity (of stone)
= vertical component (because velocity vector is inclined) at 45∘ with horizontal.
Therefore (ucosθ)=gt−(usinθ) ...(iii)
The right hand side is written gt−usinθ because the stone is in its downward motion.
Therefore, gt>usinθ
In upward motion usinθ>gt
Multiplying equation (iii) with t we can write,
(ucosθ)t+(usinθ)t=10t2 ...(iv)
Now (iv)−(ii)−(i) gives 4.25t2−4.25=0 or t=1s
Substituting t=1s in (i) and (ii) we get
usinθ=6.25m/s
⇒uy=6.25m/s and ucosθ=3.75m/s
⇒ux=3.75m/s therefore →u=uxˆi+uyˆj
⇒→u=(3.75ˆi+6.25ˆj)m/s
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - MCQ with one or more than one correct Question
1 Video
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stone will meet.
View SolutionA stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25ms.Calculate when and where the two stones will meet.
View Solution
Knowledge Check
A body starts from rest from the origin with an acceleration of 3m/s(2) along the x-axis and 4m/s2 along the y-axis. Its distance from the origin after 2s will be
A5mB10mC15mD20mA body starts from rest from the origin with an acceleration of 6m/s2 along the x-axis and 8m/s2 along the y-axis. Its distance from the origin after 4 seconds will be
A56 mB64mC80 mD128mAn object starts from rest at the origin and moves along the x axis with a constant acceleration of 4m/s2. Its average velocity as it goes from x=2 m to x=8 m is :
A2 m/sB3 m/sC5 m/sD6 m/s
A stone is dropped from a height of 100m .At the same instant another stone is projected vertically upwards with velocity of 50ms^(-1) .If g=10ms^(-2) ,the height from the ground at which the 2 stones meet is
View SolutionAn object at rest at the origin begins to move in the +x direction with a uniform acceleration of 1m/s2 for 4s and then it continues moving with a uniform velocity of 4 m/s in the same direction. The x-t graph for object's motion will be -
View SolutionA body starts from rest from the origin with an acceleration of 6m/s2 along x axis and 8m/s2 along y axis.The distance from origin after 4 seconds will be
View SolutionThe acceleration of a particle moving along x-direction is given by equation a=(3−2t)m/s2. At the instant t=0 and t=6s, it occupies the same position.
(a) Find the initial velocity vo
(b) What will be the velocity at t=2s?
View SolutionAt time t=0 s a car passes a point with velocity of 16m/s and thereafter slows down with acceleration a=−0.5tm/s2 ,where t is in seconds. It stops at the instant t=
View Solution