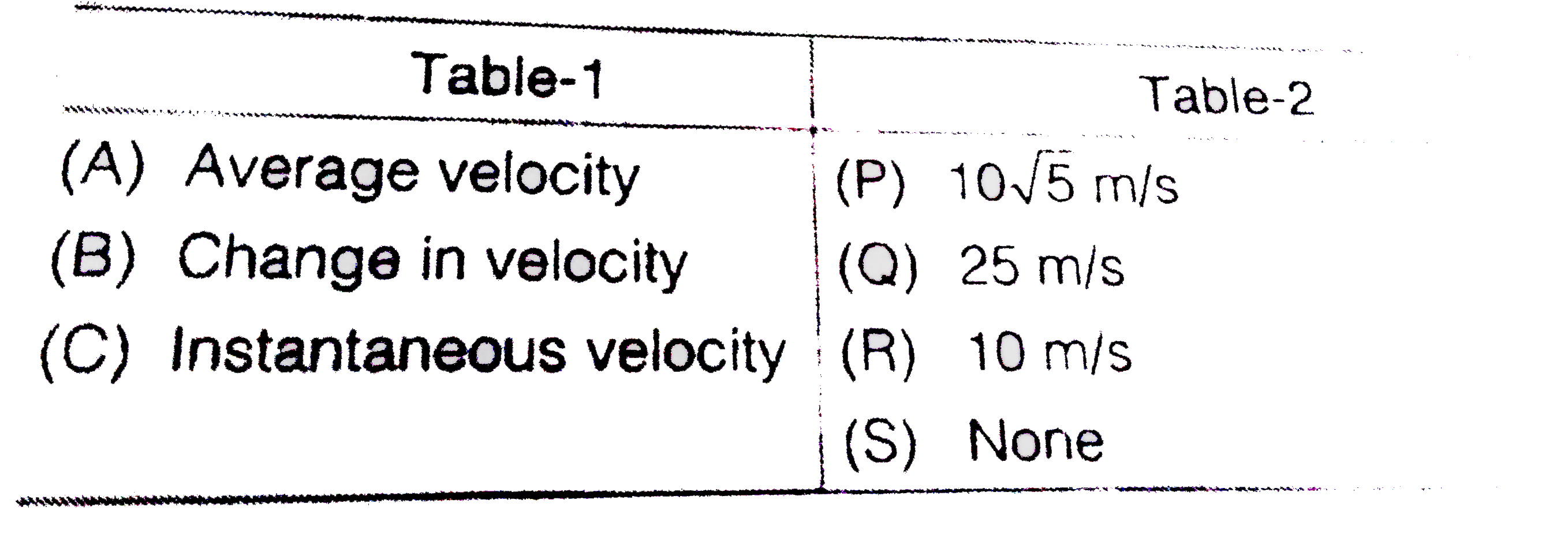As shown in the figure there is a particle of mass √3kg, is projected with speed 10m/s at an angle 30∘ with horizontal (take g=10m/s2) then match the following

Column IColumn II(A)Average velocity(in m/s)during half of the time of flight, is(P)12(B)The time (in sec after which the angle between velocity(Q)52o√13vector and initial velocity vector becomes π/2is(C)Horizonal range (in m), is(R)5√3(D)Change in linear momentum (in N-s) when particle is at(S)At an angle oftan−1(12√3)highest point, isfrom horizontal(T)2
Video Solution
Text Solution
The correct Answer is:(A)→(Q,S);(B)→(T);(C)→(R);(D)→(R)
For (A) : vav=√(vavx)2+(vavy)2=√(10cos30∘)2+(10sin30∘+02)2=√75+254=52√13m/s
Angle with horizontal θ=tan−1(vavyvavx)=tan−1(5/25√3)=tan−1(12√3)
For (B) : By using →v=→u+→at we have ugt=sin30∘⇒t=10(10)(1/2)=2
For (C) : Horizonatl range (R)=u2sin2θg=100×√3/210=5√3m
For (D) : Change in linear momentum =muy=√3×10sin30∘=5√3N−s

|
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-01
Explore 55 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-02
Explore 57 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
Knowledge Check
A particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1mA particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
A12 secB1 secC√3/2secD√3/2secA particle is projected with speed 20ms−1 at an angle 30∘ With horizontal. After how much time the angle between velocity and acceleration will be 90∘
A1 sB2 sC1.5 sDnever
If a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
View SolutionA particle is projected with a velocity of 25m/s at an angle of 30∘ with the horizontal . Calculate
(i) The maximum height ,
(ii) time of flight and
(iii) horizontal range .
View SolutionWhat are the two angles of projection of a projectile projected with velocity of 30m/s, so that the horizontal range is 45m. Take, g=10m/s2.
View SolutionA particle is projected at an angle 60∘ with the horizontal with a speed 10m/s. Then, latus rectum is (Take g=10m/s2)

View Solution