Doubtnut Promotions Sticky

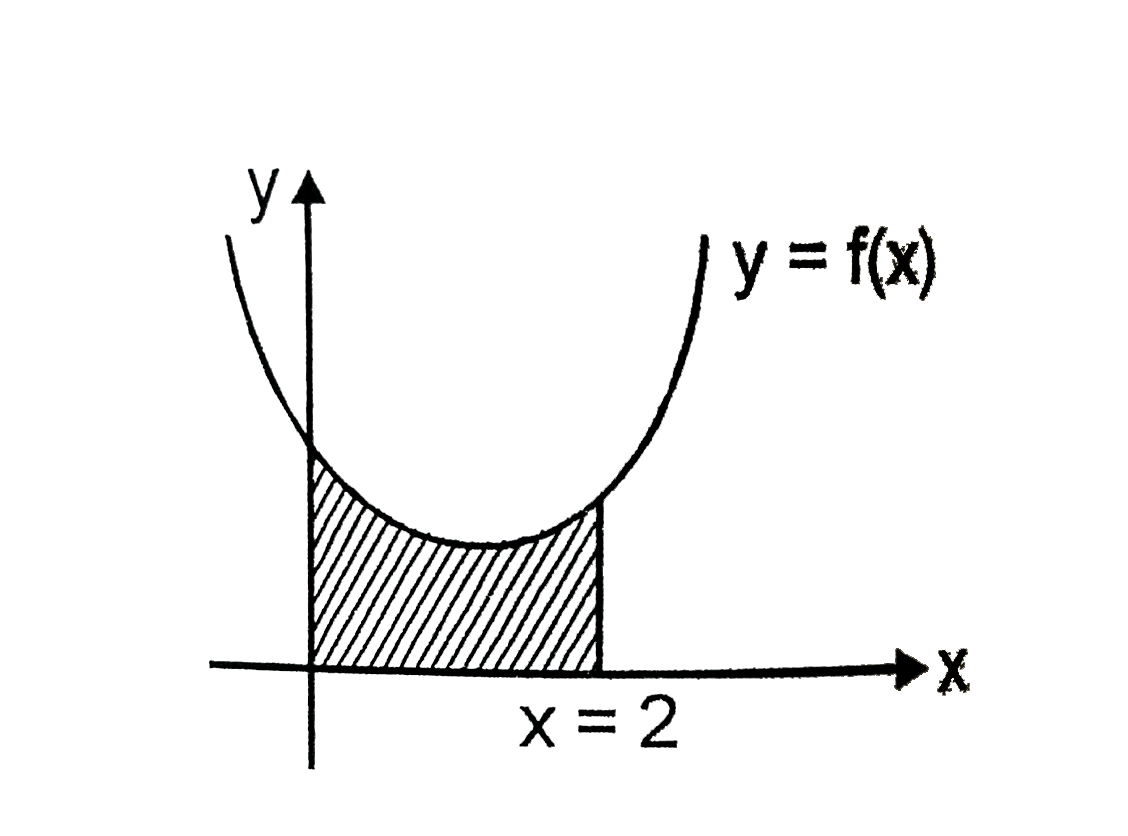
If f ( x ) = a + b x + c x 2 where c > 0 and b 2 - 4 a c < 0 . Then the area enclosed by the coordinate axes,the line x = 2 and the curve y = f(x) is given by

A

1 3 { 4 f ( 1 ) + f ( 2 ) }

B

1 2 { f ( 0 ) + 4 f ( 1 ) }

C

1 2 { f ( 0 ) + 4 f ( 1 ) + f ( 2 ) }

D

1 3 { f ( 0 ) + 4 f ( 1 ) + f ( 2 ) }

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Area = ∫ 2 0 y d x = ∫ 20 0 ( a + b x + c x 2 ) d x = 2 a + 2 b + 8 c 3
= 1 3 ( 6 a + 6 b + 8 c )
= 1 3 { f ( 0 ) + 4 f ( 1 ) + f ( 2 ) }
ocr_image

|
Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    If f(x)=a+bx+cx2 where c > 0 and b2−4ac<0. Then the area enclosed by the coordinate axes,the line x = 2 and the curve y = f(x) is given by

    A13{4f(1)+f(2)}
    B12{f(0)+4f(1)}
    C12{f(0)+4f(1)+f(2)}
    D13{f(0)+4f(1)+f(2)}
  • Question 2 - Select One

    If f(x)=a+bx+cx2 where a,b,c∈R then ∫1of(x)dx

    A(13)(f(1)+f(0)+2f(12))
    B(16)(f(1)+f(0)+4f(12))
    C(16)(f(1)+f(0)−4f(12))
    D(16)(f(1)−f(0)−4f(12))
  • Question 3 - Select One

    Let f(x)=ax2+bx+c, where a∈R+ and b2−4ac<0. Area bounded by y=f(x), x-axis and the lines x = 0, x = 1, is equal to :

    A16(3f(1)+f(−1)+2f(0))
    B112(5f(1)+f(−1)+8f(0))
    C16(3f(1)−f(−1)+2f(0))
    D112(5f(1)−f(−1)+8f(0))