A square ABCD of diagonal length 2a, is folded along the diagonal AC so that the planes DAC, BAC are at right angles. The shortest distance between DC and AB is
√2a
2a/√3
2a/√5
None
The correct Answer is:C
Let
f(x)=x(lnx−1)
f(x)=lnx
f''(x)=1x , e∫1((f''+f)sinx)dx
Use integration by parts =∫f''.sinx+∫f.sinx
=sinx.f']e1−∫cosx.f'+f.(−cosx)]e1−∫f'.(−cosx)=sinx.lnx]e1−x(lnx−1).(cosx)]e1
Topper's Solved these Questions
Similar Questions
Knowledge Check
A square ABCD of diagonal length 2a, is folded along the diagonal AC so that the planes DAC, BAC are at right angles. The shortest distance between DC and AB is
A√2aB2a/√3C2a/√5DNoneIn a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
In the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
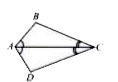
View SolutionWhich of the following statements are true for a square? It is a rectangle. It has all its sides of equal length. Its diagonals bisect each other at a right angle. Its diagonals are equal to its sides.
View SolutionIf the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
View SolutionIf the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
View SolutionThree statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?
View Solution
