Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
1
4
0
None of these
The correct Answer is:C
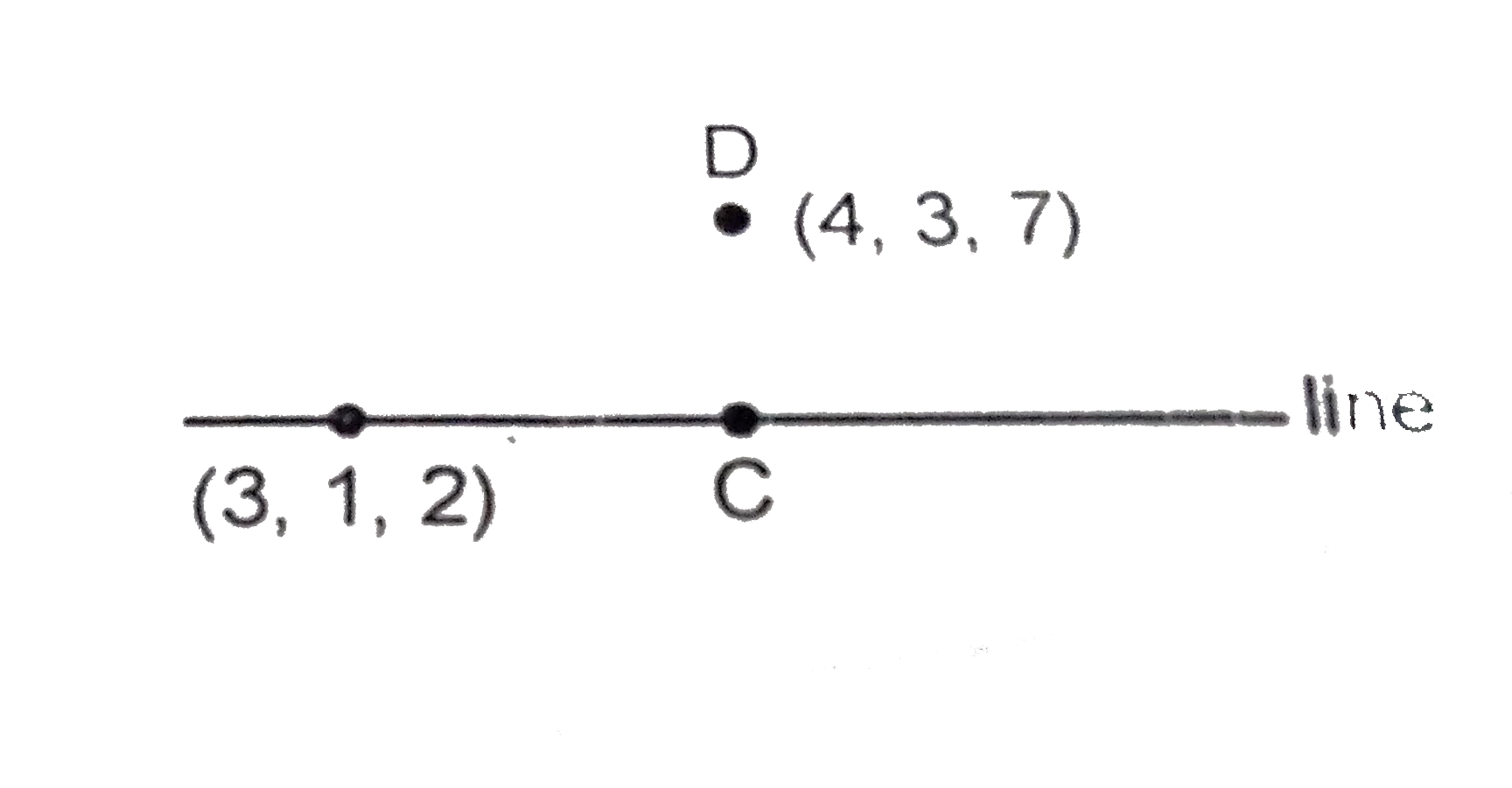
Point on line C(3+2λ,1+4λ,2+5λ)
DR's of DC (2λ−1,4λ−2,5λ−5)
DC⊥line
∴λ=79⇒DR'sofDC(59,109,−109)
Equation of plane : 59(x−3)+109(y−1)−109(z−2)=0
∴ Equation of plane x+2y−2z=1
Topper's Solved these Questions
Similar Questions
Consider a tetrahedron with faces f1,f2,f3,f4. Let →a1,→a2,→a3,→a4 be the vectors whose magnitudes arerespectively equal to the areas of f1,f2,f3,f4 and whose directions are perpendicular to these faces in theoutward direction. Then
View SolutionFind magnitude and direction of →F2−→F1 if →F1=500N due east and →F2=250N due north:
View Solution
Knowledge Check
Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
A1B4C0DNone of theseIf ∣∣→V1+→V2∣∣=∣∣→V1−→V2∣∣ and V2 is finite, then
AV1 is parallel to V2B→V1=→V2CV1 and V2 are mutually perpendicularD∣∣→V1∣∣=∣∣→V2∣∣If |vecV_1+vecV_2|=|vecV_1+vecV_2|andV_2 is finite, then
AV1 is parallel to V2B→V1=→V2CV1 and V2 are mutually perpendicularD∣∣→V1∣∣=∣∣→V2∣∣
Let →u,→v,→w be such that |→u|=1,|→v|=2,|→w|=3. If the projection of →v along i is equal to that of →w along ¯u and vectors →v,→w are perpendicular to each other then |→u−→v+→w| equals
View SolutionA vector is by →V=(8.0ˆi+2.0ˆj)m/s. What will be direction of unit vector perpendicular to →V?
View SolutionIf F1andF2 aare two vectors of equal magniudes F such that |F1.F2|=|F1×F2|,then|F1+F2| equals to
View SolutionLet →u,→vand→w be such that |→u|=1,|→v|=2and|→w|=3 if the projection of →v along h→u is equal to that of →w along →u and vectors →vand→w are perpendicular to each other then |→u−→v+→w| equals
View SolutionA frame of reference F2 moves with velocity →v with respect to another frame F1. When an object is observed from both frames, its velocity is found to be →v1 in F1 and →v2 is equal to
View Solution