Six long parallel current carrying wires are perpendicular to the plane of the fig. They pass through the vertices of a regular hexagon of side length a. All wires have same current I. Direction of current is out of the plane of the figure in all the wires except the one passing through vertex F, which has current directed into the plane of the figure. Calculate the magnetic induction field at the centre of the hexagon. Also tell the direction of the field.

The correct Answer is:μ0Iπa towards midpoint of DE
Step by step video, text & image solution for Six long parallel current carrying wires are perpendicular to the plane of the fig. They pass through the vertices of a regular hexagon of side length a. All wires have same current I. Direction of current is out of the plane of the figure in all the wires except the one passing through vertex F, which has current directed into the plane of the figure. Calculate the magnetic induction field at the centre of the hexagon. Also tell the direction of the field. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
In the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
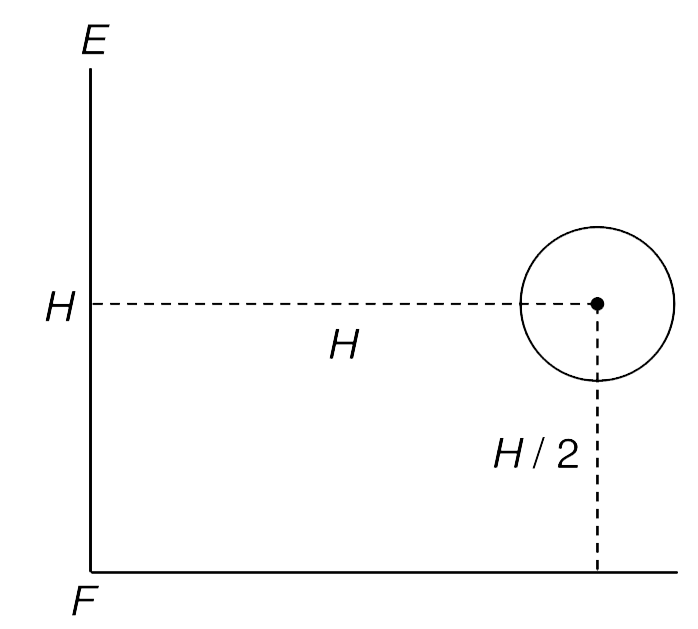 02:40View Solution
02:40View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
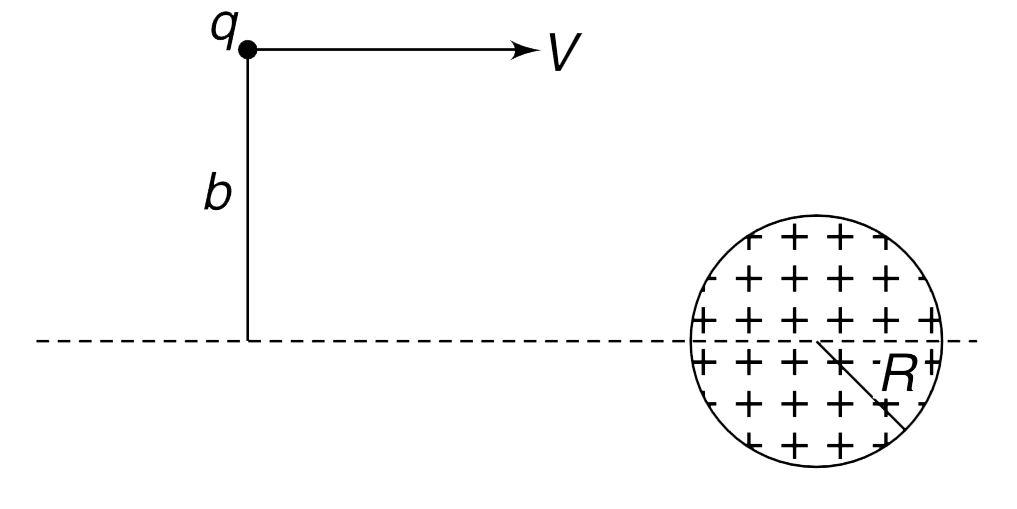 03:57View Solution
03:57View SolutionA rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current I is established in the wire as shown in the figure ,
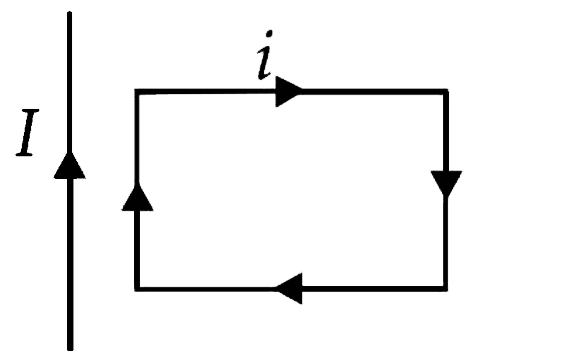 09:55View Solution
09:55View SolutionA long copper wire carries a current of I ampere. Calculate the magnetic flux per meter of the wire for a plane surface S inside the wire as shown in Fig.
01:55View SolutionTwo infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as
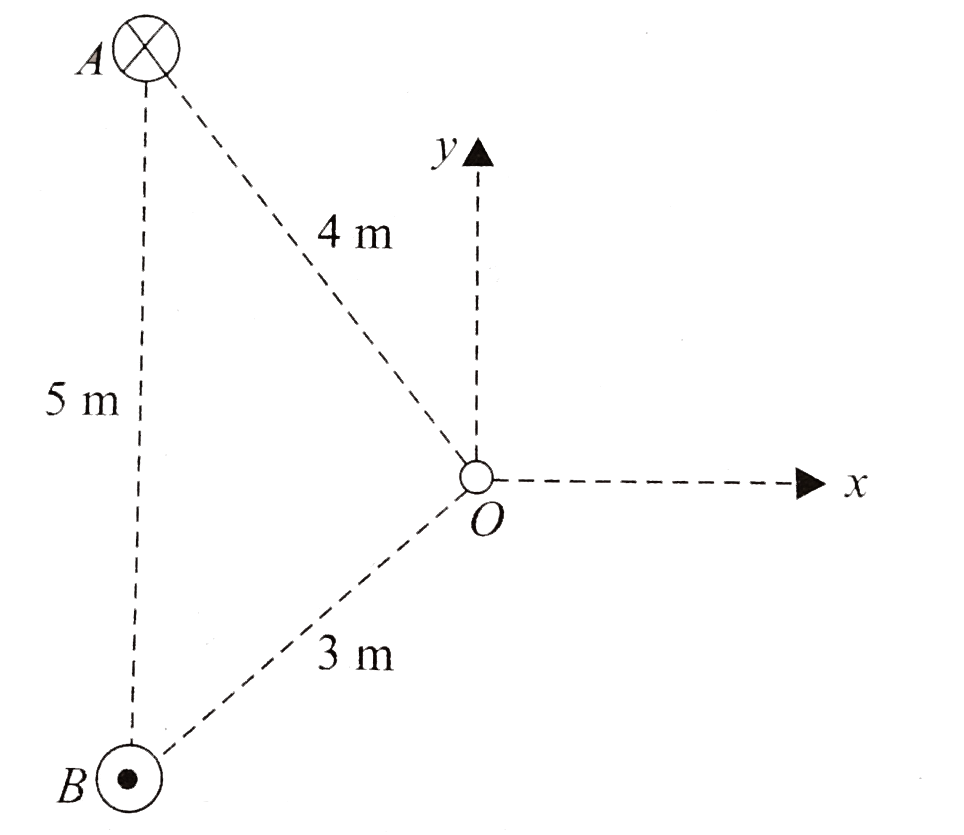 08:01View Solution
08:01View SolutionSketch the magnetic field lines in xy plane for a pair of long parallel wires laid along z direction if-
(a) Both wires carry current in same direction.
(b) Both wire carry current in opposite directions.06:42View Solutionfigure 4.22 shows two long wires A and B, each carrying a current I, separated by a distance l and oriented in a plane perpendicular to the plane of paper. The directions of currents are shown in figure. Find the magnetic induction at a point P located at a distance l from both wires as shown in figure4.22
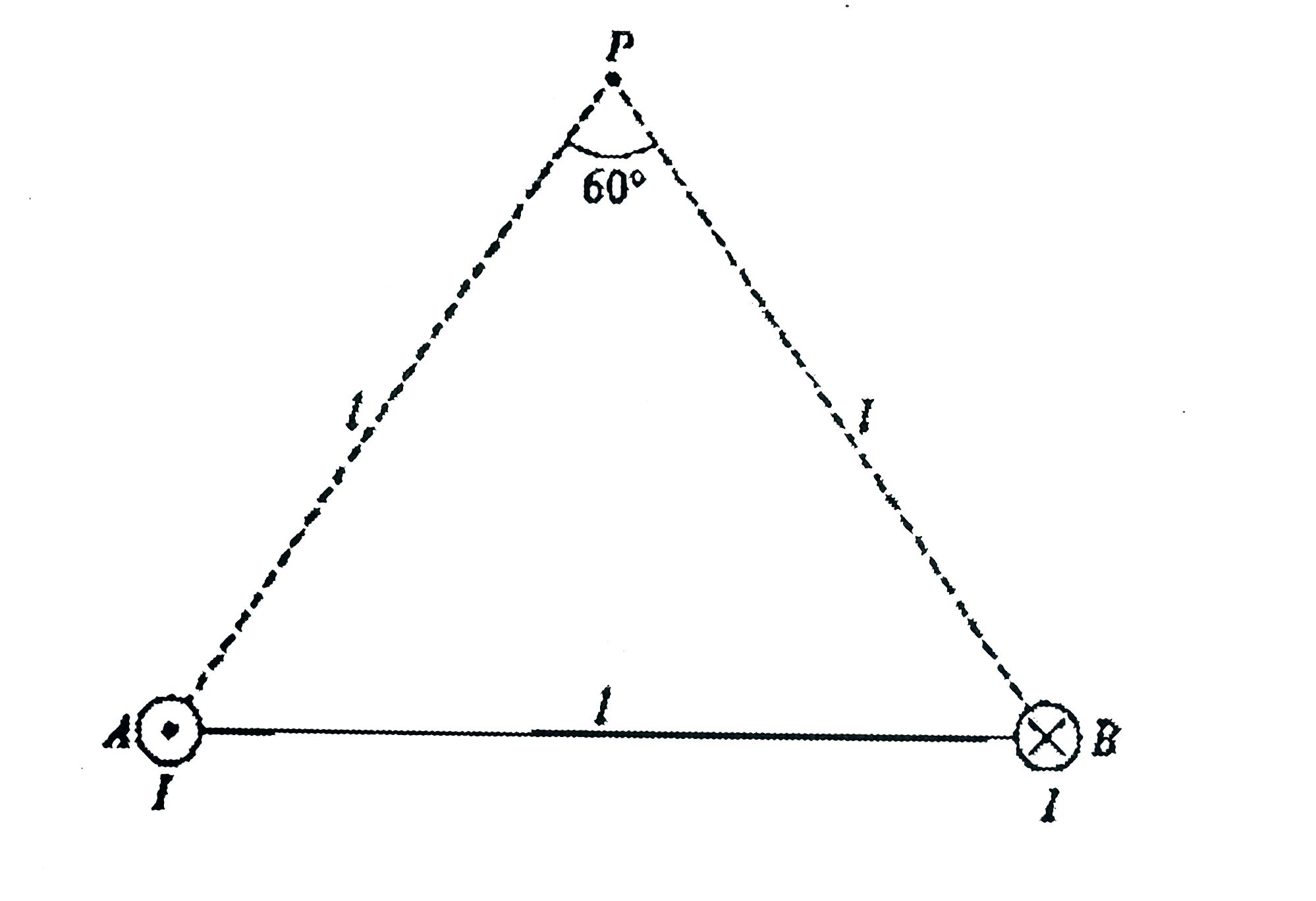 01:37View Solution
01:37View SolutionA long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
02:38View SolutionA current-carrying straight wire is held in exactly vertical position. If the current passes through this wire in the vertically upward direction, what is the direction of magnetic field produced by it ? Name the rule used to find out the direction of magnetic field.
07:16View SolutionA rectangular loop carrying a current i_(2) situated near a long straight wire carrying a steady current i_(1) . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
06:31View SolutionEqual currents passing through two infinitely long parallel wires. Would there be any magnetic field midway between the wires, if the currents are (i) in the same direction, (ii) in opposite directions?
07:03View SolutionA current carrying wire (current = i) perpendicular to the plane of the paper produced a magnetic field, as shown in the figure. A square of side a is drawn with one of its vertices on the wire. The integral ointvecB.dvecr along PQR has the value
01:26View SolutionA rectangular loop carrying a current i1, is situated near a long striaght wire carrying a steady current i2. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
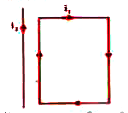 05:36View Solution
05:36View SolutionA rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current I is established in the wire as shown in the figure ,
08:11View SolutionA long copper wire carries a current of I ampere. Calculate the magnetic flux per meter of the wire for a plane surface S inside the wire as shown in Fig.
04:28View Solution

