The power radiated by a star and its mass ma are related by where and are power radiated by the Sun and mass of the Sun respectively. Assume that the fraction of mass lost by the star since its birth is . Calculate the age of the star in terms of and .
The correct Answer is:
To solve the problem, we start with the given relationship between the power radiated by a star (P) and its mass (m):
PP0=(mM0)7/2
Where P0 is the power radiated by the Sun and M0 is the mass of the Sun. We need to express the age of the star in terms of the fraction of mass lost (α), the mass of the Sun (M0), the power of the star (P), and the power of the Sun (P0).
Step 1: Express the mass of the star in terms of its initial mass and the fraction lost
Assuming the fraction of mass lost by the star since its birth is α, we can express the current mass m of the star as:
m=M0(1−α)
Step 2: Substitute m into the power equation
Substituting m into the power equation gives:
PP0=(M0(1−α)M0)7/2
This simplifies to:
PP0=(1−α)7/2
Step 3: Rearranging to find α
We can rearrange this equation to express α:
1−α=(PP0)2/7
Thus,
α=1−(PP0)2/7
Step 4: Relate mass loss to age
The rate of mass loss can be expressed as:
dmdt=−kP
Where k is a proportionality constant. The total mass lost over time can be integrated to find the age of the star t:
∫mM0dm=−kP∫t0dt
This gives:
M0−m=−kPt
Step 5: Substitute for m
Substituting m=M0(1−α):
M0−M0(1−α)=−kPt
This simplifies to:
M0α=−kPt
Step 6: Solve for age t
Rearranging gives:
t=−M0αkP
Step 7: Express k in terms of known quantities
Assuming k is a constant that can be expressed in terms of M0 and P0, we can express the age of the star as:
t=M0αP0P
Final Expression
Thus, the age of the star in terms of α, M0, P, and P0 is:
t=M0αP0P
Assuming the fraction of mass lost by the star since its birth is α, we can express the current mass m of the star as:
Substituting m into the power equation gives:
We can rearrange this equation to express α:
The rate of mass loss can be expressed as:
Substituting m=M0(1−α):
Rearranging gives:
Assuming k is a constant that can be expressed in terms of M0 and P0, we can express the age of the star as:
Thus, the age of the star in terms of α, M0, P, and P0 is:
Topper's Solved these Questions
Similar Questions
if power P and linear mass density are related as P=αβ2+λ2, then find the dimensions of α and β
View SolutionA neutron star has a density equal to that of the nuclear matter. Assuming the staar to be spherical, find the radius of a neutron star whose mass is 4.0×1030kg (twice the mass of the sun ).
View Solution
Knowledge Check
An ideal gas equation can be written as P=ρRTM0 where ρ and M are resp.
ANumber density , molar massBMass density , molar massCNumber density , mass of the gasDMass density , mass of the gas0.1 M NaCl and 0.1 M CH3COOH are found to have osmotic pressures of P1 and P2 respectively then what is the correct ststement ?
AP1>P2BP1ifP2CP1ltP2DP1=P2=0 atm.Two short dipoles pˆk and P2ˆk are located at (0,0,0) & (1m,0,2m) respectively. The resultant electric field due to the two dipoles at the point (1m,0,0) is
A9p32π∈0ˆkB−7p32π∈0ˆkC7p32π∈0ˆkDnone of these
Assuming the atomic mass of a metal M to be 56, calculate the empirical formula of its oxide containing 70.0% M.
View SolutionOne mole of a diatomic gas undergoes 'a process P=P01+(VV0)s, where P0,V0 are constants. The translational kinetic energy of the gas when V=V0 is given by αP0V0β, Find (α+β).
View SolutionDensity of a neutron star is 2.7×1017kgm−3. Assume the star to be spherical, calculate the radius of the neutron star if its mass is twice the mass of the sun. Take mass of the sun =2.0×1030kg
View SolutionMasses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
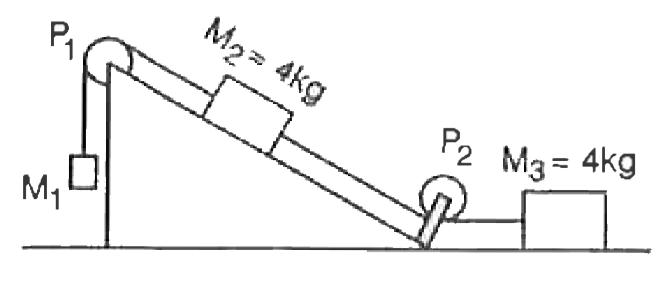
View SolutionDistance between the centres of two stars is 10a. The masses of these stars are M and 16M ans their radit a nd 2a respectively. A body of mass m is fired straight from the surface of the larger star tpwards the surface of the smaller star. What should be its minimum intial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and a.
View Solution
