A uniform quarter circular thin rod of mass M and radius R is pivoted at a point B on the floor. It can rotate freely in the vertical plane about B. It is supported by a smooth vertical wall at its other free end A so that it remains at rest. Find the reaction force of wall on the rod.
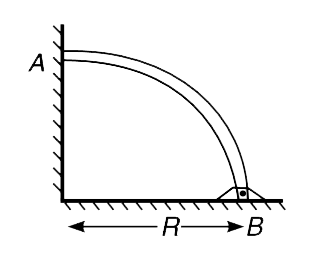
The correct Answer is:N=(1−2π)Mg
Step by step video, text & image solution for A uniform quarter circular thin rod of mass M and radius R is pivoted at a point B on the floor. It can rotate freely in the vertical plane about B. It is supported by a smooth vertical wall at its other free end A so that it remains at rest. Find the reaction force of wall on the rod. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
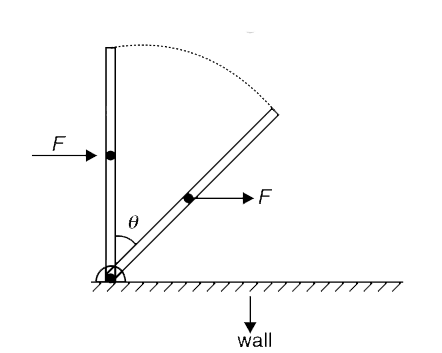
A uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity).
(a) With what angular speed will the rod hit the wall ?
(b) At what angle θ (see figure) the hinge force will make a 45∘ angle with the rod ?
View SolutionA uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius R=L3 is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
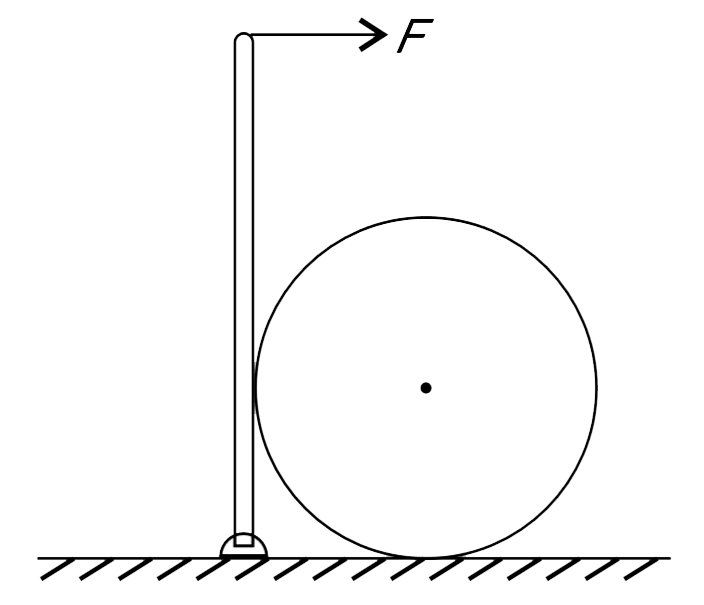
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting.
View Solution
Knowledge Check
A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
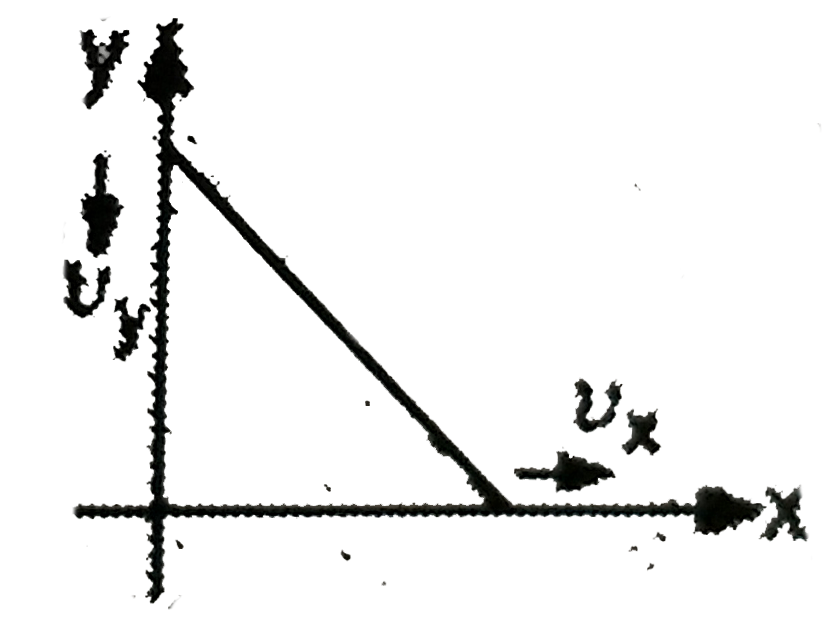 AThe other end also moves uniformlyBThe speed of other end goes on decreasingCThe speed of other end goes on increasingDThe speed of other end first decreases and then increases
AThe other end also moves uniformlyBThe speed of other end goes on decreasingCThe speed of other end goes on increasingDThe speed of other end first decreases and then increasesA slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
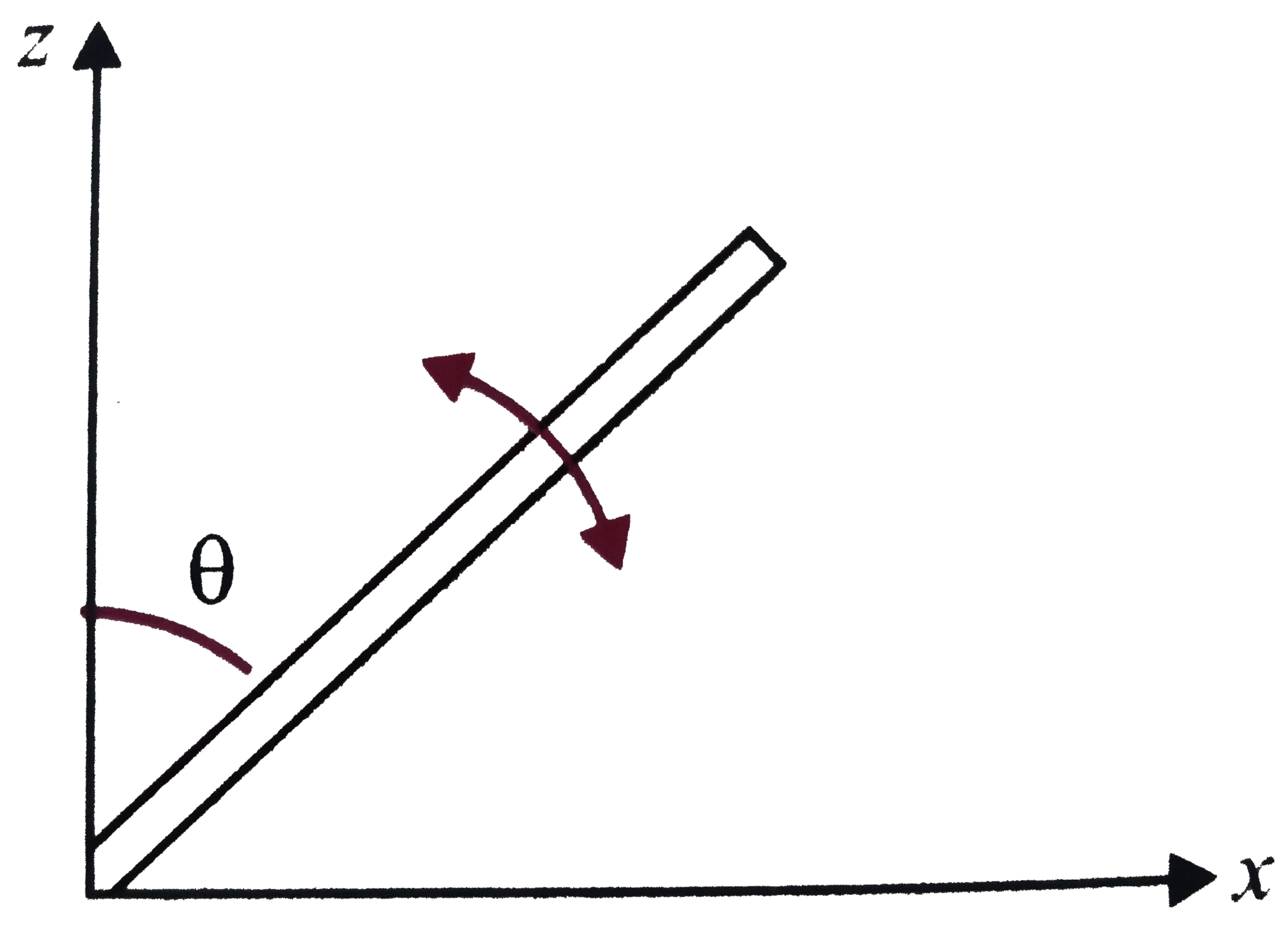 A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθ
A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
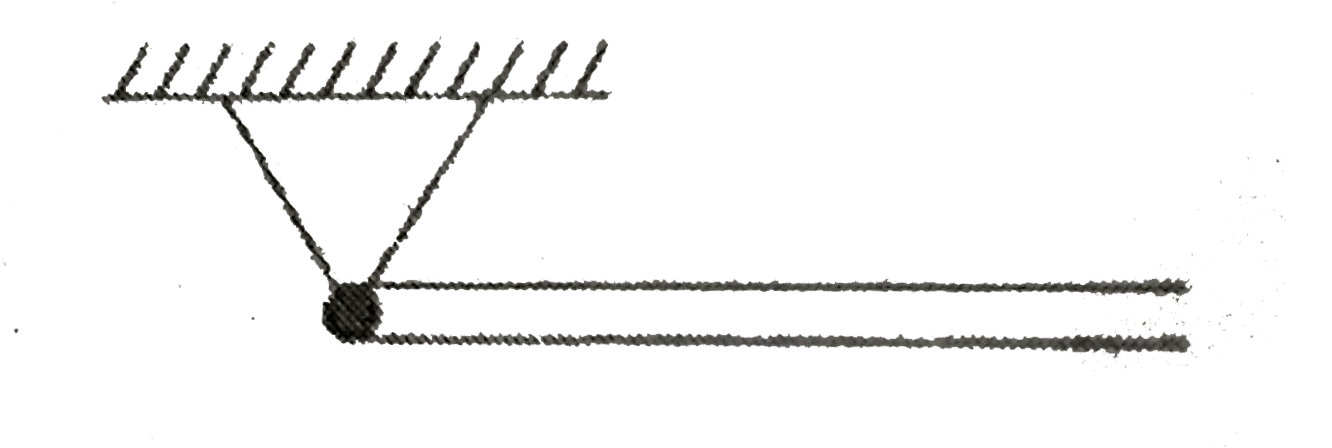 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15
A thin rod of mass M and length a is free to rotate in horizontal plane about a fixed vertical axis passing through point O. A thin circular disc of mass M and of radius a/4 is pivoted on this rod with its center at a distance a/4 from the free end so that it can rotate freely about its vertical axis. Assume that both rod and disc have uniform density and they remain horizontal during motion. An outside stationary observer finds the rod rotating with an angular velocity Ω and the disc rotating about its vertical axis with angular velocity 4Ω. Total angular momentum of system about point O is (Ma2Ω48)n. The value of n is
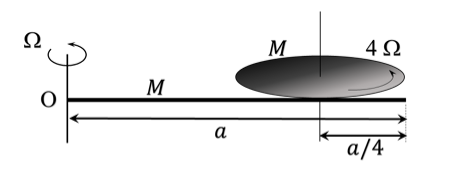
View SolutionA uniform rod of mass M and length L is hinged at its lower end so as to rotate freely in the vertical plane of the fig. There is a small tight fitting the hinged end. A small mass less pin welded to the rod supports the bead. The system is released from the vertical position shown. It was observed that the bead just begins to slide on the rod when the rod becomes horizontal.
(a) Find the normal contact force between the rod and the bead when the rod gets horizontal. What is the direction of this force?
(b) Find the coefficient of friction between the bead and rod.

View SolutionA light rigid rod has a bob of mass m attached to one of its end. The other end of the rod is pivoted so that the entire assembly can rotate freely in a vertical plane. Initially, the rod is held vertical as shown in the figure. From this position it is allowed to fall. (a) When the rod has rotated through θ=30∘ , what kind of force does it experience– compression or tension? (b) At what value of θ the compression (or tension) in the rod changes to tension (or compression)?
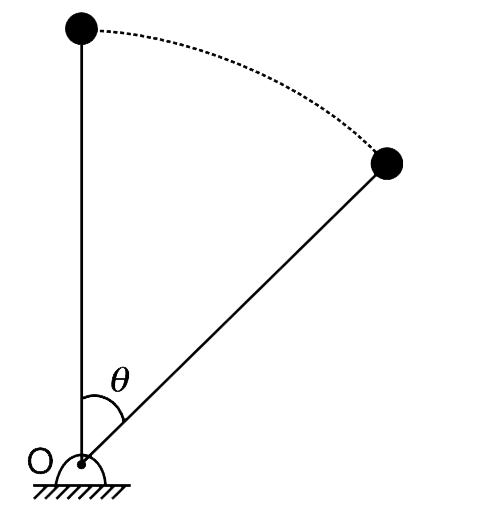
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
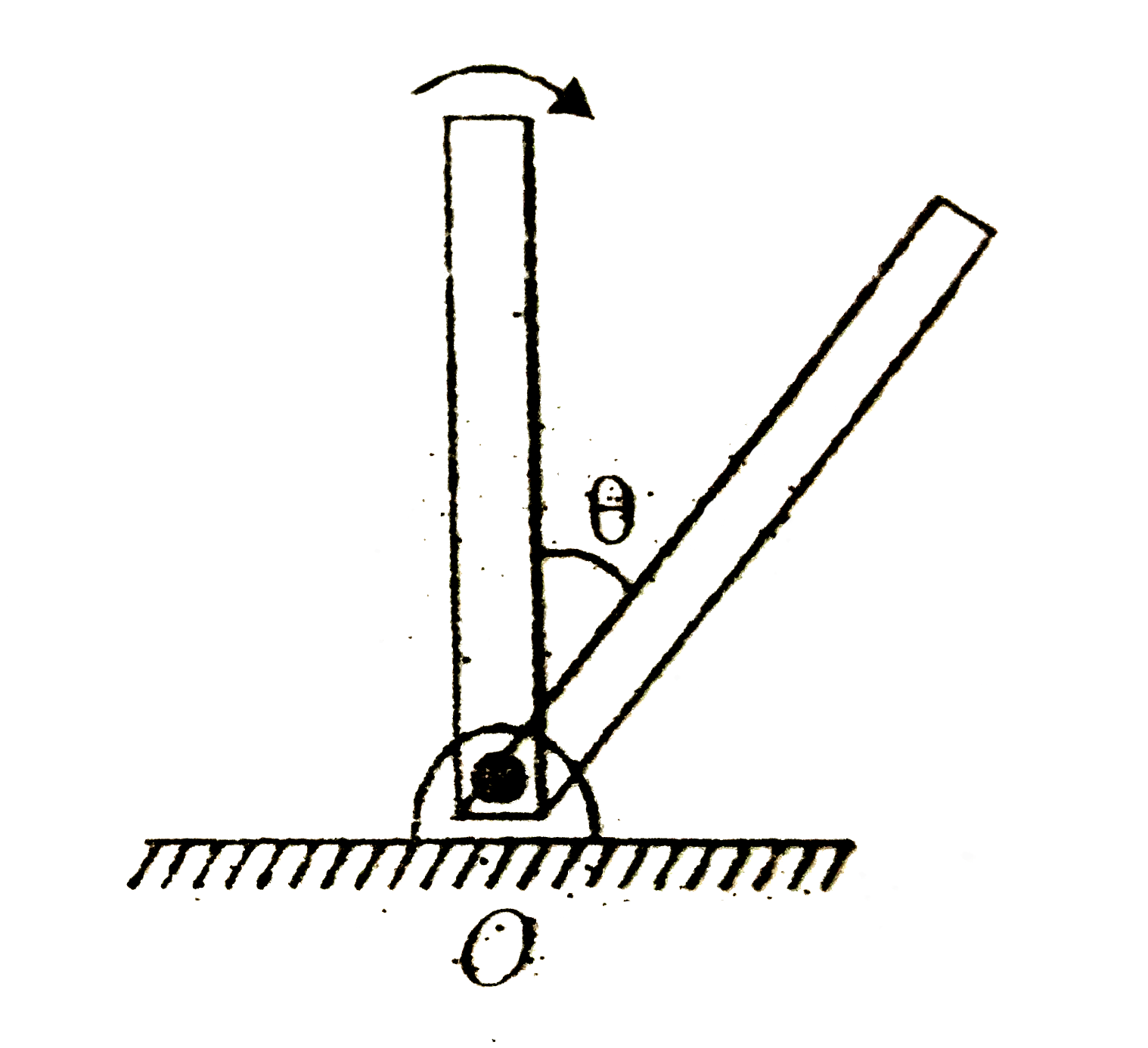
View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View Solution
