A ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
The correct Answer is:Slightly less than 6 m/s
Step by step video, text & image solution for A ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
A ball of mass m approaches a wall of mass M (M>>m), with speed 2 ms−1 along the normal to the wall. The speed of wall is 1 ms−1 towards the ball. The speed of the ball after an elastic collision with the wall is-
View SolutionA ball of mass 'm' strikes a rigid wall with speed 'u' and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
View SolutionA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 View Solution
View SolutionA ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If mass of the wall is taken as infinite, then the work done by the ball on the wall is
View SolutionA ball of mass m is moving normally towards a walll of mass M(>>m) with the velocity 4m/s. The wall is also moving. After striking elastically with the wall , velocity of ball becomes 8m/s. Find the speed of the wall:
View SolutionA ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
View SolutionA particle of mass m is projected towards a wall such that theangle of incidence is θ and the speed just before collision is u. Assumming that the wall is smooth and the collision is elastic,show that the ball rebonunds at same angle.
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
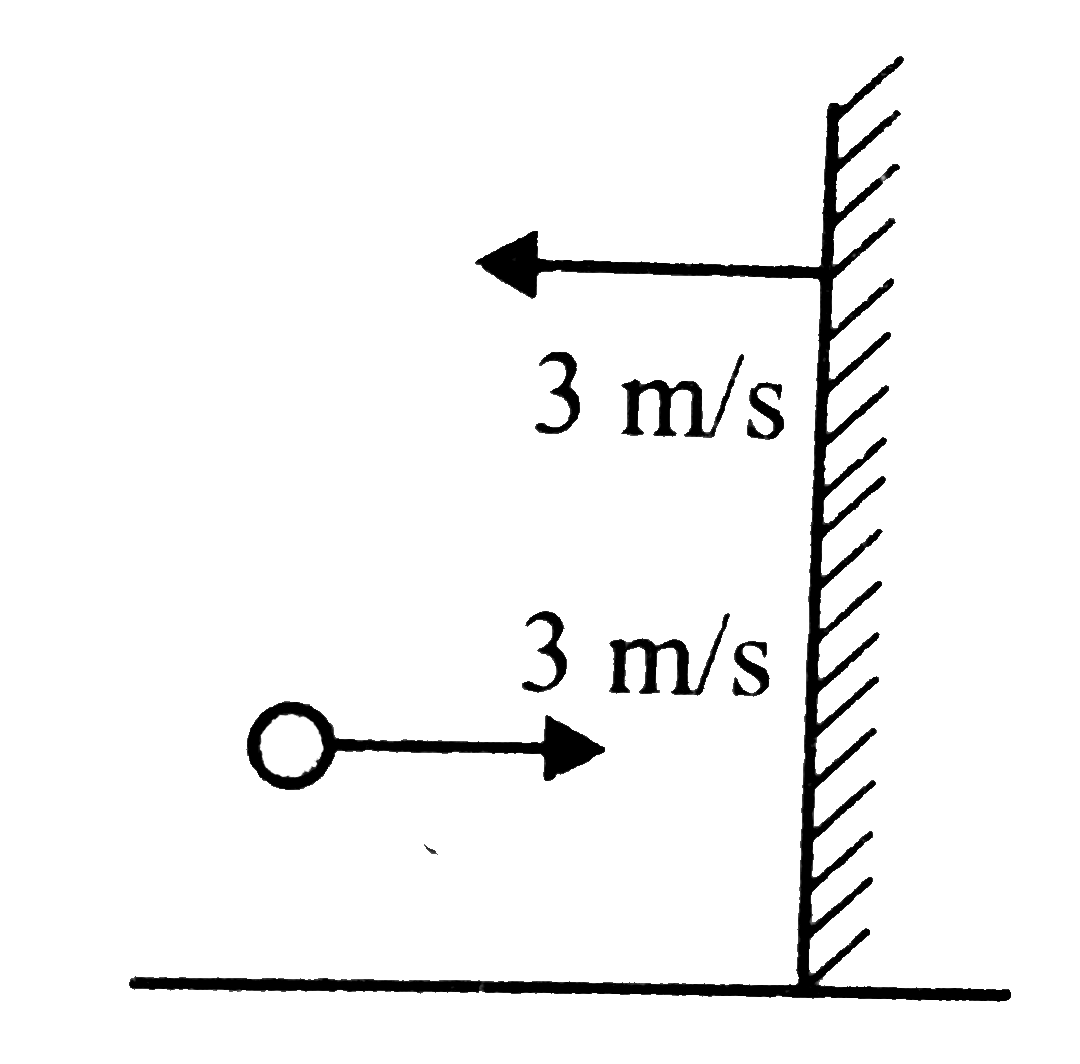 View Solution
View SolutionA ball of mass 'm' collides with a wall with speed 'V' and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
View Solution


